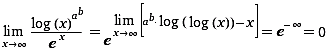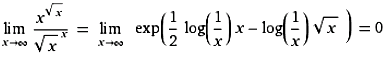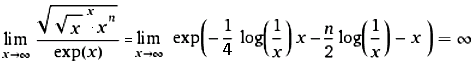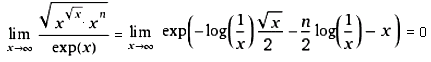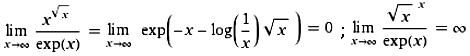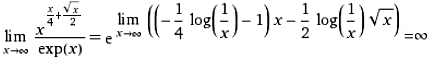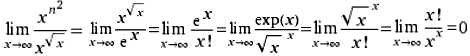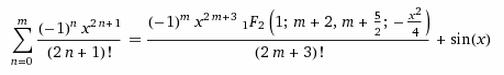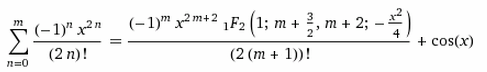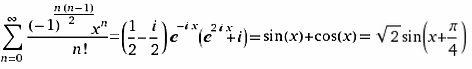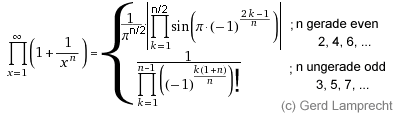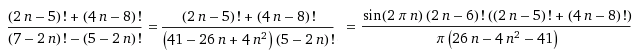Nichttriviale Grenzwerte (Non-trivial limits; Gerd Lamprecht) |
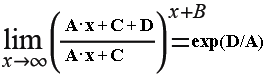 ;
; 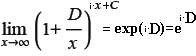 ;
;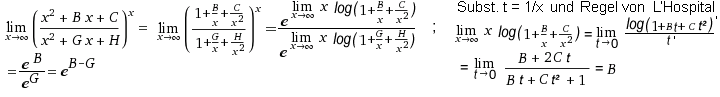
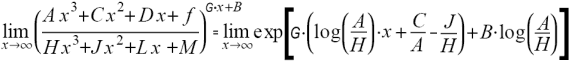
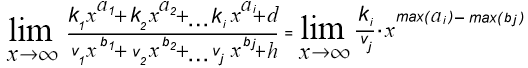 ; d.h.:
; d.h.: 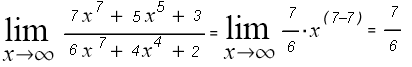 ;
;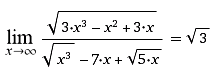
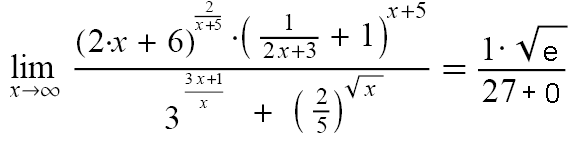
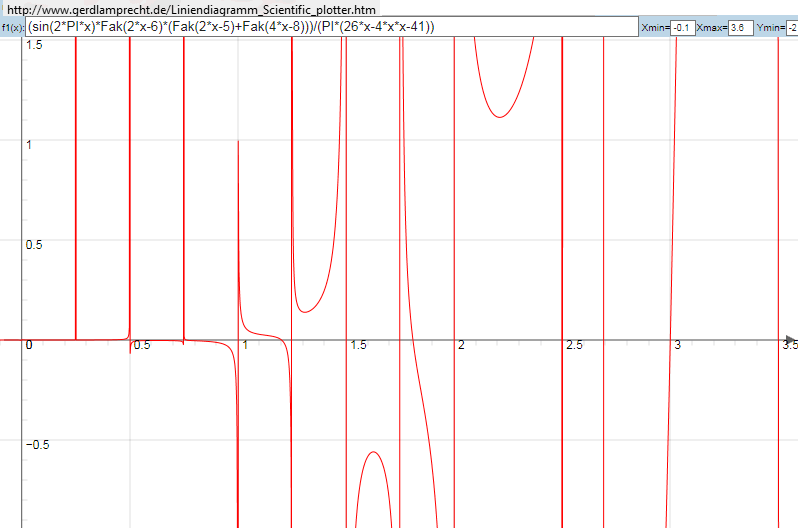
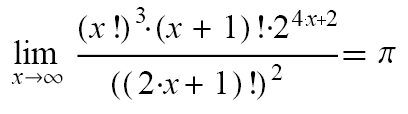 ein Bruch, der Pi im Unendlichen (also nie) erreicht!
ein Bruch, der Pi im Unendlichen (also nie) erreicht!
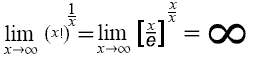 ;
; 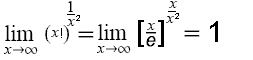
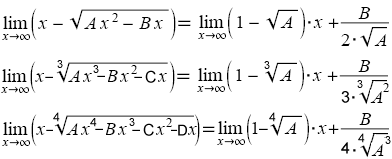
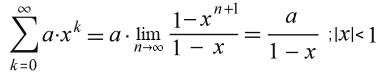
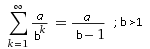
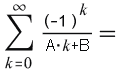 Lerch(-1,1,B/A)/A= hyg2F1(1,B/A,B/A+1,-1)
Lerch(-1,1,B/A)/A= hyg2F1(1,B/A,B/A+1,-1)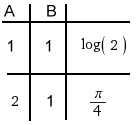
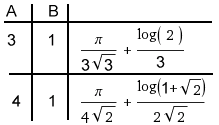
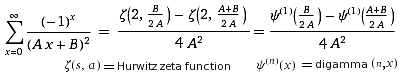 ; Zeta(2,y) = PolyGamma(1,y) = hyg3F2[1,y,y, y+1,y+1,1]/y²
; Zeta(2,y) = PolyGamma(1,y) = hyg3F2[1,y,y, y+1,y+1,1]/y²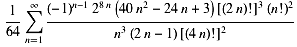 = hyg3F2(1,1/2,1/2,3/2,3/2,-1)= Beta(2,Dirichlet)=A006752=0.915..=Catalan's Konst.
= hyg3F2(1,1/2,1/2,3/2,3/2,-1)= Beta(2,Dirichlet)=A006752=0.915..=Catalan's Konst. 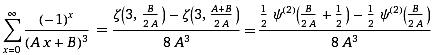
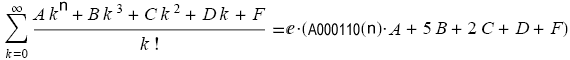 siehe A000110
siehe A000110
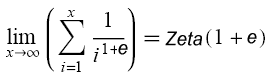 =1.10461783244907976840066196... siehe Zeta(x) Wissenschaftlicher Online Rechner mit Umkehrfunktionen
=1.10461783244907976840066196... siehe Zeta(x) Wissenschaftlicher Online Rechner mit Umkehrfunktionen
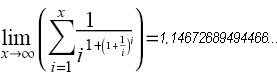
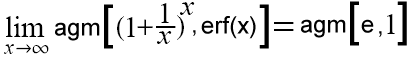 = A191503 = 1.7523515580810808267140866648...
= A191503 = 1.7523515580810808267140866648...
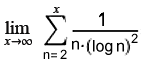 = A115563 = 2.1097428012368919744792571976...
= A115563 = 2.1097428012368919744792571976...
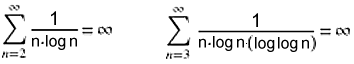
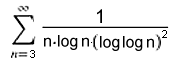 = A118582 = 38.4067680928217... {10^(3.14*10^86) Summanden für 2 Stellen!}
= A118582 = 38.4067680928217... {10^(3.14*10^86) Summanden für 2 Stellen!}
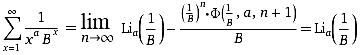 = PolyLog(a,1/B)
; B=1 und a<=1 ergibt ∞
= PolyLog(a,1/B)
; B=1 und a<=1 ergibt ∞
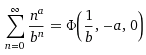 =LerchPhi(1/b,-a,0) ; |b|>1
=LerchPhi(1/b,-a,0) ; |b|>1
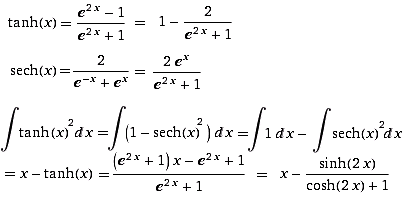
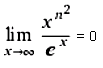 analog
analog