Benchmarks: Lösung Linearer Gleichungssysteme (Matrixform)

Home...

Warum nicht Typ float (etwa 8 Dezimalstellen genau): bei 50 x 50 ist Probe nur 4 Stellen genau; 90 x 90: 2 Stellen; 100 x 100: 0

4131 x 4131 Gleichungssystem double Zahlen ohne In- & Outputzeiten (15 Stellen; Probe stimmen 8...10 Stellen)

https://de.wikipedia.org/wiki/Lineares_Gleichungssystem#Matrixform

Erg=Inverse(M)•B

Hardware:

i9-7900X , 4.3 GHz, 32 GB RAM, Win10

Berechnungszeit

Software / Sprache

Version/Code/Befehl

Bemerkung

Multithreading

Timeout

py\sympy

Erg=solve_linear_system(Mat,*symb)

200 x 200 in 102 s

Timeout

SAGE online

M.inverse()*B; 500 x 500 in 91.6 s

200 x 200 in 5.9 s

Error!

MAXIMA 5.27.0 (12.04.0)

x: linsolve(M,b);

200 x 200 in 10.5 s

nein

3484.21 s

GP/PARI V. 2.11.1

\p14 ; matsolve(M,B)

200 x 200 in 0.172 s

nein

764.08 s

EXCEL-VBA ohne Ausgabe

MMult(WorksheetFunction.MInverse(M), B)

mehr als 52 x 52!!

nein

300.00 s

SAGE online\numpy

linalg.solve(M,B) ; online Timeout!

3k x 3k in 28.5 s

nein

69.62 s

c++ eigen-3.4.0

MatrixXd.bdcSvd(...).solve(b)

nein

44.00 s

c++ AVX2; 2D Array

siehe Code-LinSolver-cpp.htm

mit float 20 s

nein

33.97 s

c++ eigen-3.4.0

calc + FullPivLU.lu.solve(b);

copy 0.1 s

nein

14.95 s

onlinegdb.com \ R

system.time(Erg <- solve(M, B))

10.62 s

c++ LAPACK 3.7.0

LaLinearSolve(M, x, B);

MinGW-> MSVC

nein

4.18 s

c++ eigen-3.4.0

calc + SparseLU.solve(b);

besser = statt insert

nein

3.16 s

c++ eigen-3.4.0

calc + SparseLU.solve(b);

besser = AVX2 fast

nein

1.55 s

Mathematica 11.3

Erg = Inverse[M].B;

nur zum Vergleich

> 10 Threads

1.20 s

maple\nzimme10

time[real](LinearSolve(M, B))

0.80 s

Julia V. 1.7.2

@time sol = solve(LinearProblem(M, B))

> 10 Threads

0.74 s

Mathematica 12.0

Erg = Inverse[M].B;

> 10 Threads

0.70 s

c++ eigen-3.4.0

PartialPivLU lu(M);lu.solve(b);

besser = AVX2 fast

20 Threads

0.41 s

Mathematica 11.3

Erg = LinearSolve[M,B];

nur 1 Befehl

> 10 Threads

0.31 s

py\numpy 1.26.4

Erg=np.linalg.solve(M,B)

10k x 10k in 3.4 s

> 10 Threads

0.30 s

Mathematica 12.0

Erg = LinearSolve[M,B];

10k x 10k in 2.68 s

> 10 Threads

0.178..0.3 s

Julia V. 1.10.3

@time sol = solve(LinearProblem(M, B))

10k x 10 k in 1.498 s

16 Threads

500 x 500 Lin. Gleichungssystem; ohne In- & Outputzeiten (50 Stellen genau; Probe 45..47 Stellen richtig)

https://de.wikipedia.org/wiki/Lineares_Gleichungssystem#Matrixform

Erg=Inverse(M)•B

Hardware:

i9-7900X , 4.3 GHz, 32 GB RAM, Win10

Berechnungszeit

Software / Sprache

Version/Code/Befehl

Bemerkung

Multithreading

nur double!

onlinegdb.com \ R

options(digits=22); Erg <- solve(M, B)

nur 10 richtige NK!

also ist 22 Täuschg.

791.64 s

MAXIMA 5.27.0 (12.04.0)

bfloat; x: linsolve(M,b);

200 in 130.24 s

1 Thread

275.60 s

py\mpmath dps=50

Erg=mp.lu_solve(M,B)

1 Thread

269.80 s

py\mpmath dps=51

for R in range(0,I):F = m[R][I]/m[I][I]…

eigener Gauß Code

1 Thread

90.34 s

maple\nzimme10

time[real](LinearSolve(M, B))

82.60 s

SAGE online

M.inverse()*B;

63.50 s

py\gmpy2 precision=171

for R in range(0,I):F = m[R][I]/m[I][I]…

eigener Gauß Code

1 Thread

51.60 s

SAGE\ N(..,digits=genau)

M.echelon_form()

Erg=letzte Spalte!

19.94 s

Mathematica 12.0

Inverse[M].B

1 Thread

17.78 s

Mathematica 12.0

RowReduce[M];(B in letzter Spalte)

Erg=letzte Spalte!

1 Thread

15.90 s

Julia V. 1.10.3\BigFloat

@time sol = solve(LinearProblem(M, B))

1 Thread

2.87 s

GP/PARI V. 2.11.1

\p51 ; matsolve(M,B)

1 Thread

0.15 s

Mathematica 12.0

Erg = LinearSolve[M,B];

16 Threads

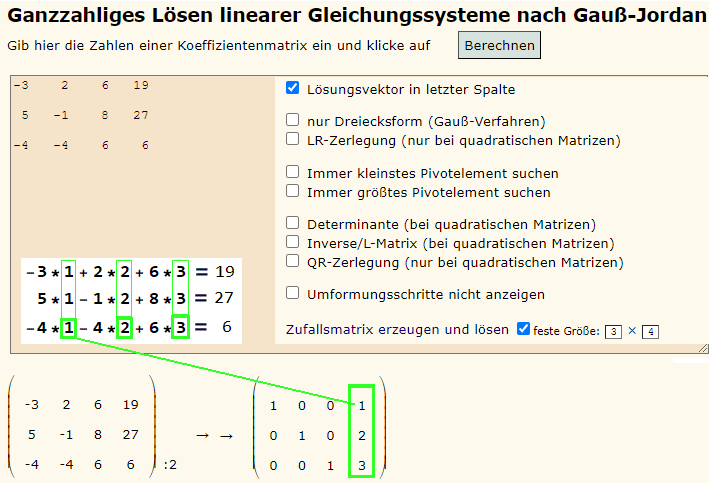
https://www.arndt-bruenner.de/mathe/scripts/gaussjordan.htm

Beispiel mit 3 x 3 Matrix:

Stand: 16.06.2024