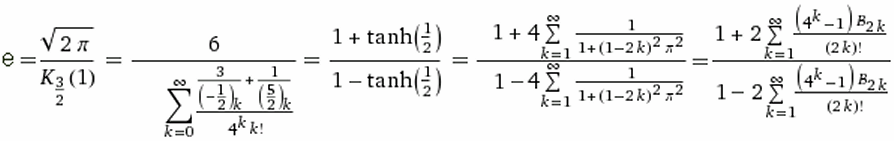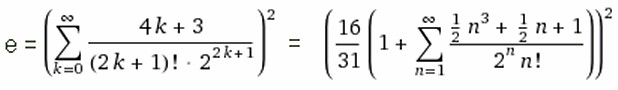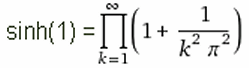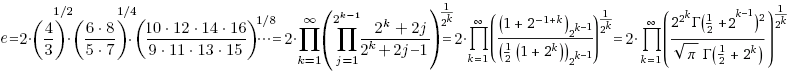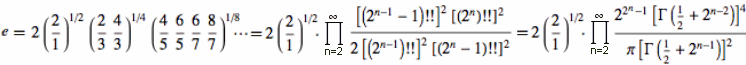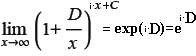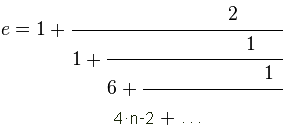"Eulersche Zahl" = A001113 - was über Wikipedia hinausgeht (Gerd Lamprecht):(Euler's number, also Napier's constant; but not Euler–Mascheroni constant A001620=0.57721566490153286060651209...)Basis des natürlichen Logarithmus = GetKoDezi(1113,0,55) = e = 2.71828182845904523536028747135266249775724709369995957... |