a[1] = -(n*x-1)
a[2] = (n+1)*x*(n*x-2)+1
a[3] = -((n+2)*x*((n+1)*x*(n*x-3)+3)-1)
a[4] = ((n+3)*x*((n+2)*x*((n+1)*x*(n*x-4)+6)-4)+1)
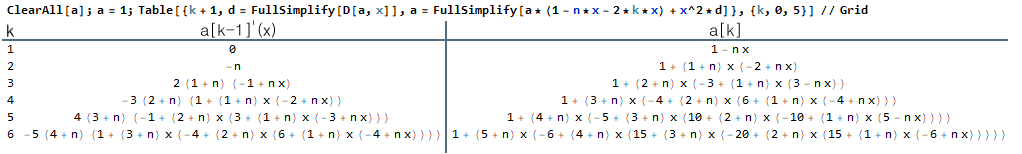 |
||
a[k]'(x) =k*(1 - k - n)*a[k - 1](x)
eingesetzt ergibt das
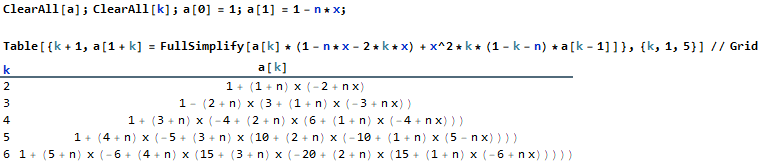
 |
||
 |
||
 |
||
Suche nach expliziten Algorithmen für eine komplizierte Rekursionsfunktion |
| Quelle der Aufgabe: matheplanet.com | |||||||
| geg.: | |||||||
| a[0] = 1 a[1] = -(n*x-1) a[2] = (n+1)*x*(n*x-2)+1 a[3] = -((n+2)*x*((n+1)*x*(n*x-3)+3)-1) a[4] = ((n+3)*x*((n+2)*x*((n+1)*x*(n*x-4)+6)-4)+1) |
|||||||
| ges.: a[k](x) besser a[k,x,n] rekursiv & explizit | |||||||
| Die ersten Schritte bis Beitrag No.8 überspringe ich mal & verweise auf | |||||||
| wikipedia.org/wiki/Rekursion | |||||||
| Algorithmus a1: a[k+1](x) = (1-n*x-2*k*x)*a[k](x) + x²*a[k]'(x) | |||||||
| Probe: | |||||||
|
|||||||
| Dank der FullSimplify
Darstellung kann man erkennen, dass die Ableitung zum Teil bereits in a[k-1]
enthalten ist: a[k]'(x) =k*(1 - k - n)*a[k - 1](x) eingesetzt ergibt das |
|||||||
| Algorithmus a2: a[1 + k](x) = a[k](x)*(1 - n*x - 2*k*x) + x^2*k*(1 - k - n)*a[k - 1](x) | |||||||
| Probe: | |||||||
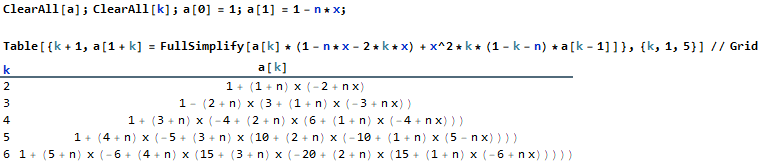
|
|||||||
| Ein Versuch, mit Hilfe von Mathematica's Rsolve hieraus eine explizite Funktion zu bekommen schlägt fehl. | |||||||
| Man bekommt aber eine optimierte DifferenceRoot[Function[... -> Algorithmus a4 | |||||||
| Probe: | |||||||
|
|||||||
| In dieser FullSimplify Darstellung erkennt man, dass durch Klammern eine Rekursion mit Binomialkoeffizienten vorliegt: ...*x*(n+0)+Binom... | |||||||
| (nur von rechts nach links statt links nach rechts). Ein Vorzeichenwechsel bekommt man mit (-1)^Index oder cos(Pi*Index) | |||||||
| Mathematics's Funktion Fold[..] eignet sich gut zum Testen: | |||||||
| Algorithmus a5: a[k](x) = Fold[#1*(n + #2 - 1)*x + (-1)^(#2 + k)*Binomial[k, #2] &, (-1)^k, Range[k]] | |||||||
| Probe: | |||||||
|
|||||||
| Nach Anpassung von Fold an den Syntax von RSolve kam dann die gesuchte explizite Funktion, wobei sich Binomial herauskürzte: | |||||||
| Algorithmus a6: a[k,x,n] = ((-1)^k*(n*x^(1+k)*(k+n)!*HypergeometricPFQ[{-k},{n},1/x])*Pochhammer[1+n,-1+k])/(x*(k+n)!)] | |||||||
|
|||||||
| Beschreibung zu dieser hypergeometrischen Funktion findet man hier | |||||||
| wikipedia.org/wiki/Verallgemeinerte_hypergeometrische_Funktion | |||||||
| functions.wolfram.com/HypergeometricFunctions/Hypergeometric1F1/ | |||||||
| 1F1 kann noch mit Pochhammer und den Fakultäten weiter gekürzt werden: Hypergeometric1F1Regularized[a, b, z] == HypergeometricPFQ[{a}, {b}, z]/ Gamma[b] -> ergibt die schöne kurze explizite Funktion: | |||||||
| Algorithmus a7: a[k,x,n] = Cos[Pi*k]*x^k Gamma[k+n]*Hypergeometric1F1Regularized[-k,n,1/x] | |||||||
| Vorteile: | |||||||
| - höchste Berechnungsgeschwindigkeit | |||||||
| - Erweiterung des Gültigkeitsbereiches für die 3 Argumente (k & n waren rekursiv immer ganzzahlig -> nun wie x mindestens reell {wenn nicht sogar komplex}) | |||||||
| - durch die reellen Argumente ergeben sich völlig neue 3D-Plott Möglichkeiten | |||||||
| Geschwindigkeitsvergleiche (Benchmarks): | |||||||
| n = 19; x = 31; k = 36; | |||||||
| a1: | |||||||
| mit Ableitung a'(x) Approximation mit k=1...16: 0.025662282950292+9.18140836168791*10^-8*E^(1.07298658724611 k^1.0900000000001)s -> 1.3*10^16 in s | 421 Mio. Jahre | ||||||
| a1.1: endy hat hier enorm optimieren können (damit nun bis k=300 in 60 s möglich) | 0.1 s | ||||||
| a2: | |||||||
| erst a[k-1](x) dann einsetzen 16572628380848160369936740318859738516379590729306807877130214299802721840104962288627719609887188994283075957 | 50.58 s | ||||||
| a3: (analog zu a2, jedoch wird x und n schon vor Start der Rekursion als Zahlenwert bekannt gegeben) | |||||||
| x,n bekannt, a[k-1]Rekursion: 16572628380848160369936740318859738516379590729306807877130214299802721840104962288627719609887188994283075957 | < 1 ms | ||||||
| a4: | |||||||
| DifferenceRoot-Function 16572628380848160369936740318859738516379590729306807877130214299802721840104962288627719609887188994283075957 | < 1 ms | ||||||
| a5...a7 16572628380848160369936740318859738516379590729306807877130214299802721840104962288627719609887188994283075957 | < 1 ms | ||||||
| Da bei k=10000 immer noch kaum messbare Unterschiede auftraten, aber die Ergebnisse in die Mio. Stellen gingen (also zu viel Zeit in überlange Zahlen floss und die Algorithmus-Unterschiede | |||||||
| in den Hintergrund traten), habe ich n und x auf 2 und 3 verkleinert und k vergrößert. | |||||||
| Erst ab k um 26000 gab es messbare Unterschiede! | |||||||
| n = 2; x = 3; k = 26001; | |||||||
| a3: Rekursion aus Beitrag 11 ohne FullSimplify -> Ergebnis 115911 stellige Zahl!!! | 0.469 s | ||||||
| a4: DifferenceRoot-Function (schnellste Rekursion) -> Ergebnis 115911 stellige Zahl!!! | 0.230 s | ||||||
| a5: Fold-Iteration/Rekursion -> Ergebnis 115911 stellige Zahl!!! | 2.605 s | ||||||
| a6: hyg1F1 & Pochhammer Explizit! -> Ergebnis 115911 stellige Zahl!!! | 0.0747 s | ||||||
| a7: hyg1F1 Regular Explizit -> Sieger!!!! -> Ergebnis 115911 stellige Zahl!!! | 0.0649 s | ||||||
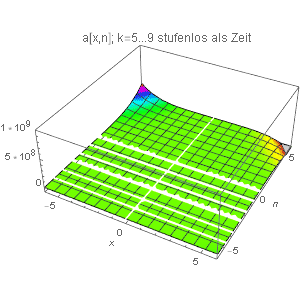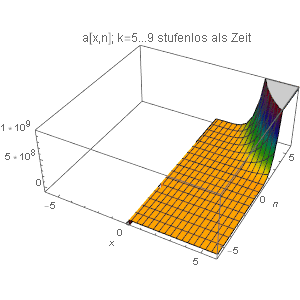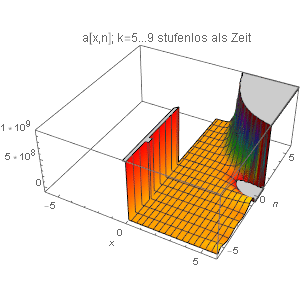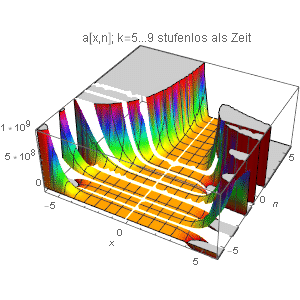
| Und nun ein 3DPlot von a[k,x,n] mit n auf der y-Achse & k als Zeit {4. Dimension} stufenlos von 5...9 mit Schrittweite 1/11: | |||||||
 |
|||||||
| Leipzig, 26.12.2020 | |||||||