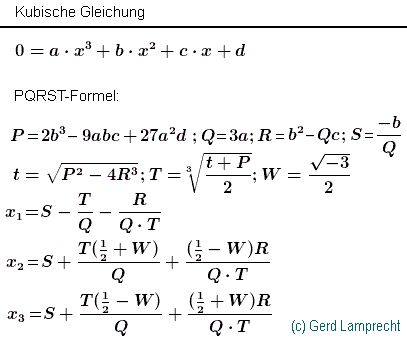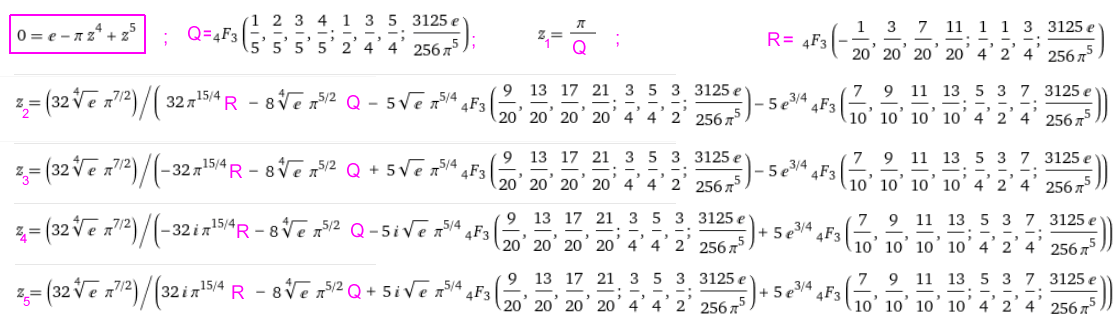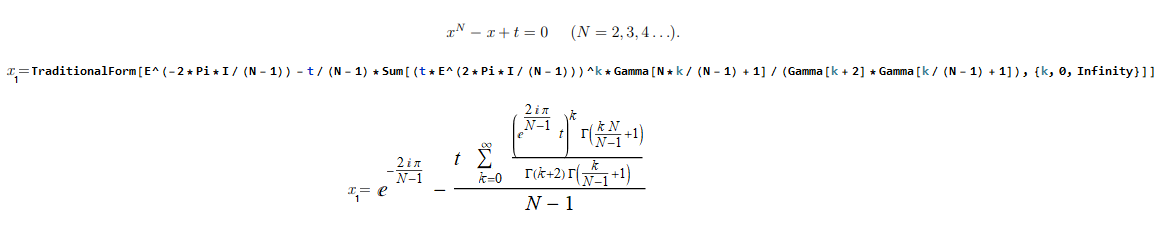|
|
|
Explizite Lösungsformeln für Polynome mit hypergeometrischen
Funktionen |
|
|
Grad 1; N=1; -> Lineare Gleichung umstellen |
|
a*x+b = 0 |
|
Lösung: x=-b/a |
|
|
Grad 2; N=2; Quadratische Gleichung; Lösung: mit p-q-Formel |
|
|
|
Grad 3; N=3; Kubische Gleichung; Lösung mit PQRST-Formel
(komplexe Zwischenergebnisse) |
|
|
|
Grad 4; N=4; Quartische Gleichung Lösung mit PQRSTUVW-Formel
(komplexe Zwischenergebnisse) |
|
https://www.lamprechts.de/gerd/php/gleichung-6-grades.php |
|
Beispiel: 1/250 - z + z^4 = 0 aus Quartische_Gleichung.html §1 als Wurzel und mit hypergeometrischer Funktion |
|
|
|
Grad 5; N=5; Quintische Gleichung vom Typ x^5 - b*x + a = 0
-> mit hypergeometrischen Funktionen |
|
|
|
Probe x^5 - 5*x + 12 = 0, also mit a=12, b=5;
Wurzelausdruck + Hypergeometrische Funktion + Newtonverfahren je 100 Stellen |
|
|
|
Grad 6; N=6; Polynom vom Grad 6, also Typ x^6-x+t -> mit
Summe und hypergeometrischen Funktionen |
|
|
|
x2 = t * HypergeometricPFQ[{1/6,1/3,1/2,2/3,5/6},{2/5,3/5,4/5,6/5},(46656 t^5)/3125] ; auch hyg5F4[...]; -> Probe mit N=6, t=1/100; Hypergeometrische Funktion + Newtonverfahren |
|
|
|
 |
|
|
|
x^6-b*x+t=0 -> x2=t*HypergeometricPFQ[{1/6, 1/3, 1/2, 2/3, 5/6}, {2/5, 3/5, 4/5, 6/5}, (46656*(t)^5)/(3125*b^6)]/b |
|
Probe: x^6-3*x+1/100,b=3,t=1/100; N[x/. Select[Solve[1/100-3 x+x^6 == 0,x], Element[x /. #1, Reals] &][[1]],55]= 0.003333333333333790580704161327409815953667850540553706666 |
|
N[1/100*HypergeometricPFQ[{1/6, 1/3, 1/2, 2/3, 5/6}, {2/5, 3/5, 4/5, 6/5 }, (46656 (1/100)^5)/(3125*3^6)]/3, 55] = 0.003333333333333790580704161327409815953667850540553706666 |
|
|
x^6-b*x^5+t=0 -> x2=b/HypergeometricPFQ[{1/6, 1/3, 1/2, 2/3, 5/6}, {2/5, 3/5, 4/5, 6/5}, (46656*(t))/(3125*b^6)] |
|
Probe: x^6-9*x^5+1/2=0;b=9,t=1/2; _____________________________...... N[Root[1/2 -9 #1^5+#1^6 &,(2)],44] =8.9999915324162625407265190702563463110558951 |
|
N[ReplaceAll[b/HypergeometricPFQ[{1/6,1/3,1/2,2/3,5/6},{2/5,3/5,4/5,6/5},46656*t/(3125*b^6)],{b->9,t->1/2}],44] =8.9999915324162625407265190702563463110558951 |
|
|
|
|
Grad 7; N=7; Polynom vom Grad 7, also Typ x^7-x+t -> per
hypergeometrischer Funktion |
|
x2 = t *
HypergeometricPFQ[{1/7,2/7,3/7,4/7,5/7,6/7},{1/3,1/2,2/3,5/6,7/6},(823543
t^6)/46656]; auch hyg6F5[...]; ->
Probe mit N=7, t=-1/10; Hypergeometrische Funktion + Newtonverfahren |
|
|
|
Grad 8; N=8; Polynom vom Grad 8, also Typ x^8-x+t -> per
hypergeometrischer Funktion |
|
x2=t
HypergeometricPFQ[{1/8,1/4,3/8,1/2,5/8,3/4,7/8},{2/7,3/7,4/7,5/7,6/7,8/7},(16777216
t^7)/823543]; auch hyg7F6[...]; ->
Probe mit N=8M t=1/250; Newtonverfahren +
Hypergeometrische Funktion |
|
|
|
|