Geometrischer Schwerpunkt (Flächenmittelpunkt; centroid; geometric center)

Die x- und y- Koordinaten des Geometrischen Schwerpunktes werden per Integral über die gesamte Fläche A berechnet:

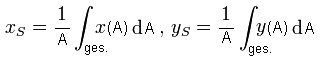
Fall: 2D Fläche unterhalb einer Kurve

mit dA = y(x)dx wird $x_{s} = \frac{1}{A}\int_a^b \! y(x) \,dx$ und $y_{s} = \frac{1}{A}\int_{f(a)}^{f(b)} \! y\cdot x(y) \,dy$
oder man nutzt aus, dass der Schwerpunkt eines jeden zur y-Achse parallelen infinitesimalen Flächenstreifen y(x)/2 ist: $y_{s} = \frac{1}{2A}\int_a^b \! y(x)^{2} \,dx$

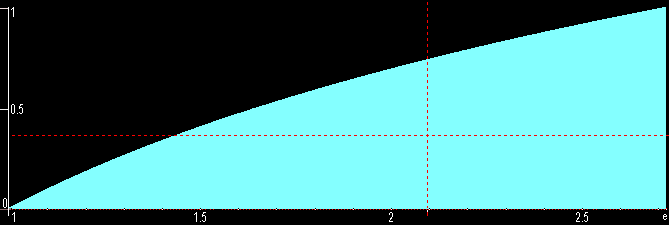
Beispiel: f(x)= log(x) von a=1 bis b=e

$A=\int_1^e \! x\cdot \log(x) \,dx=[e\cdot (\log(e)-1)]-[1 \cdot(\log(1)-1)]=1$
$x_{s} = \frac{1}{A}\int_1^e \! x\cdot \log(x) \,dx=[\frac{1}{4}e^{2}\cdot (2 \log(e)-1)]-[\frac{1}{4}1^{2}(2 \log(1)-1)]=\frac{e^{2}+1}{4}$ =2.097264024732662556807...
$y_{s} = \frac{1}{A}\int_{\log(1)}^{\log(e)} \! y\cdot (e-e^{y}) \,dy=[\frac{e \cdot y^{2}}{2}-e^{y}(y-1)]\left|\begin{matrix}1\\0\end{matrix}\right.$ $=\frac{e}{2}-0-(-e^{0}(-1))=\frac{e}{2}-1=\frac{e-2}{2}$ =0.359140914229522617680...
oder mit infinitesimalen Flächenstreifen: $y_{s} = \frac{1}{2A}\int_1^e \! \log(x)^{2} \,dx=\frac{ x (\log(x)^{2}-2 \log(x)+2)}{2}\left|\begin{matrix}e\\1\end{matrix}\right.=\frac{e-2}{2}$ =0.359140914229522617680...

Fall: beliebige 2D Fläche

Da die Funktionen x(A) und y(A) bei komplexen (unförmigen; exotischen) Gebieten (Silhouette) - wie Landkarten - nicht bekannt sind, berechnet man den Mittelpunkt (Schwerpunkt bei homogener Dichte) einer Fläche per numerischer Integration. Da Bilder im Computer als Pixel vorliegen, zählt man alle Farben, die ungleich schwarz (black=RGB(0,0,0)=NICHTS) sind, und bekommt ein pixelgenaues Ergebnis:

A=0;mx=0;my=0;
for x:=0 to maxX do
for y:=0 to maxY do if getpixel(x,y)>0 then {A:=A+1;mx:=mx+x;my:=my+y;}
Next y
Next x
xs:=mx/A; ys:=my/A;

Beispiel von oben: f(x)=log(x)

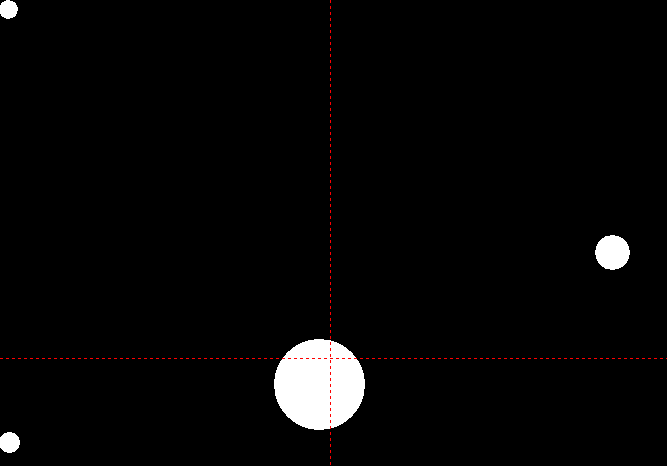
Beispiel: 4 Kreise - eine Art "Sonnensystem" mit 3 Planeten (echte Sonnen sind natürlich inhomogen und 3D):

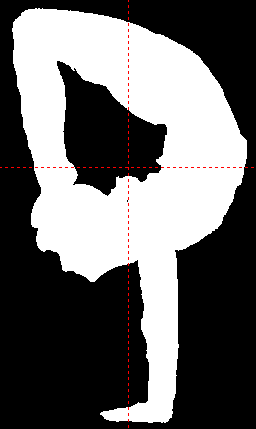
Beispiel: Frau beim Handstand mit Füße auf den Kopf:

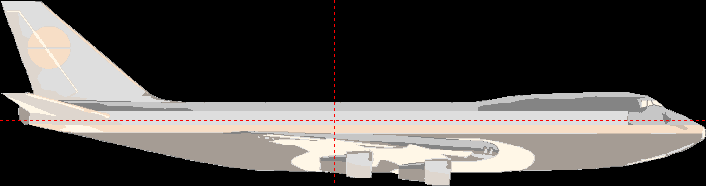
Geometrischer Flächenmittelpunkt eines Flugzeuges (Seitenansicht):

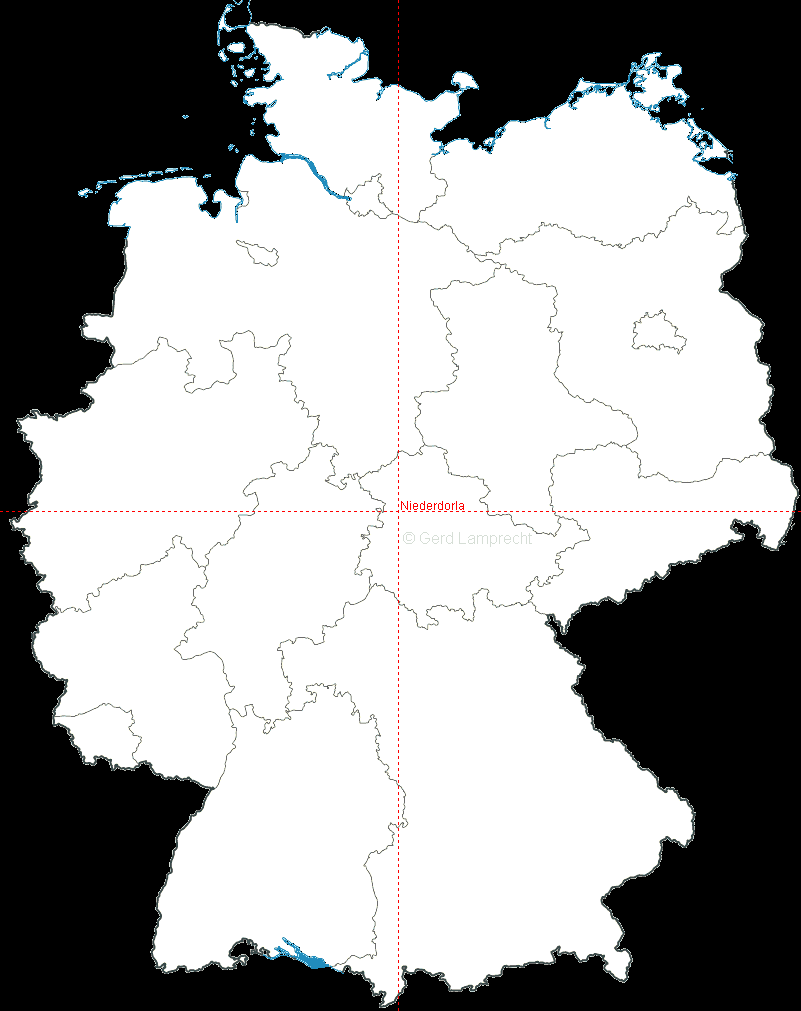
geometrischer Mittelpunkt von Deutschland bei Niederdorla (Thüringen):

Flächenmittelpunkt von Brandenburg liegt in Berlin Tempelhof:

Flächenmittelpunkt von Sachsen bei Nossen:

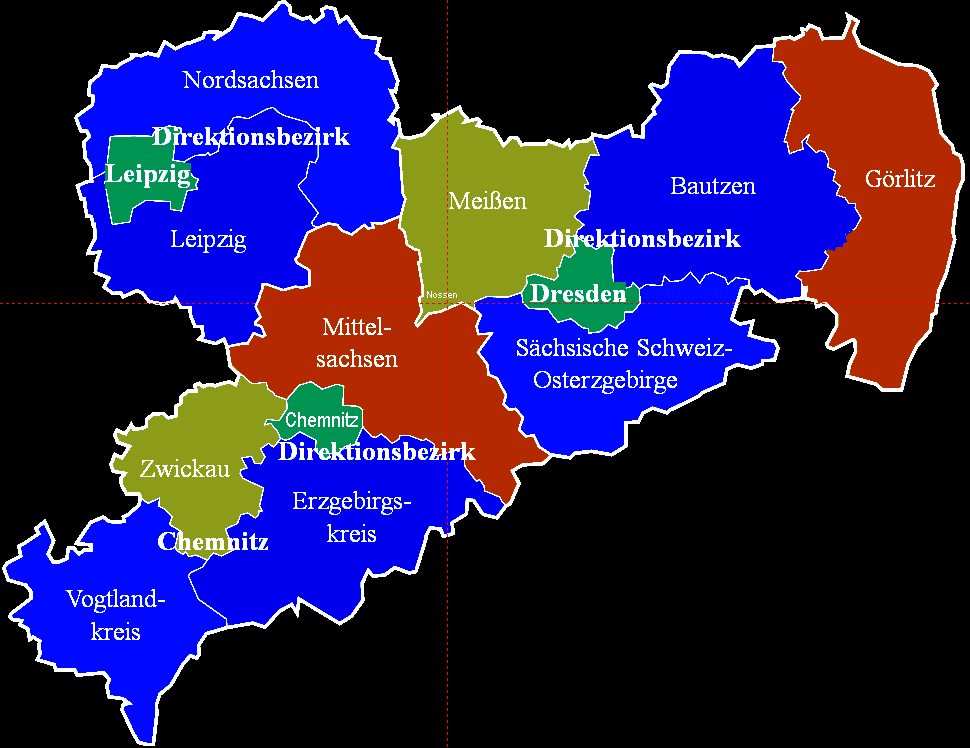
geometr. Flächenmittelpunkt von Saarland bei Eppelborn-Habach (geogr. MP bei Lebach-Falscheid) und Steiermark (bei Vorlobming):

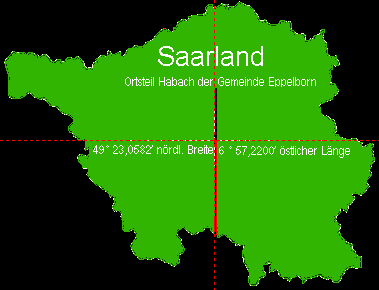
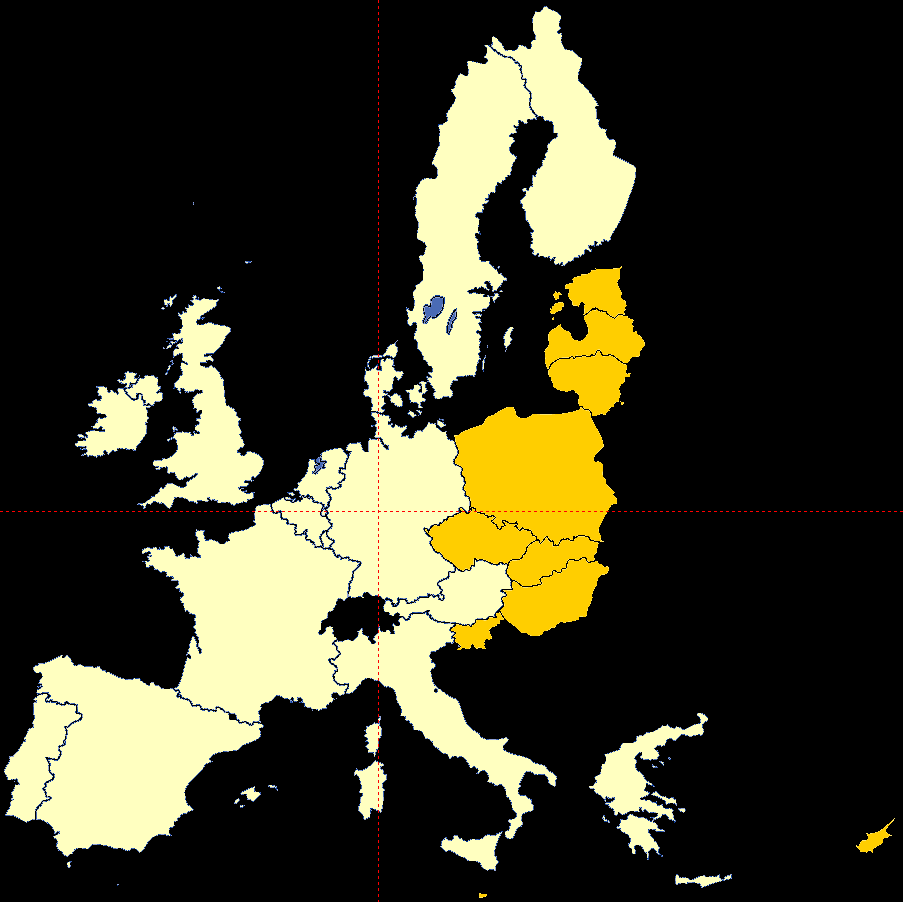
2004 lag der Flächenmittelpunkt von Europa in Deutschland (nur Staaten der EU):

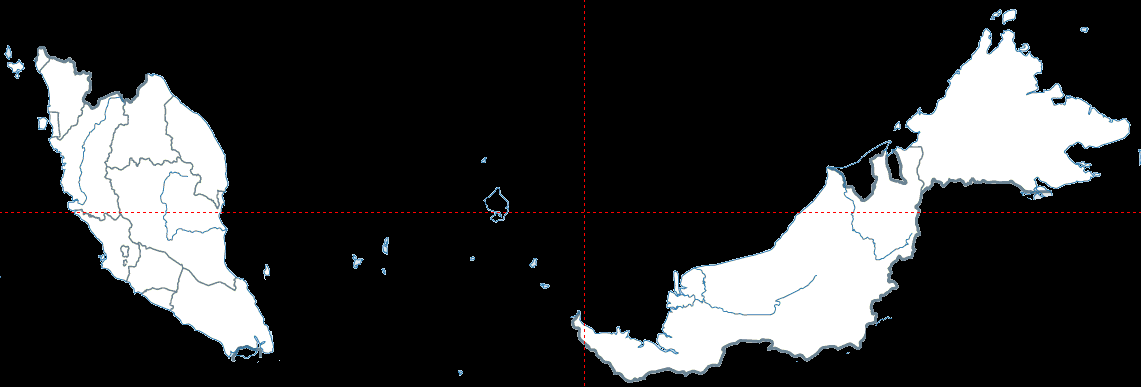
Bei Staaten wie Malaysia liegt der Flächenmittelpunkt im Wasser:

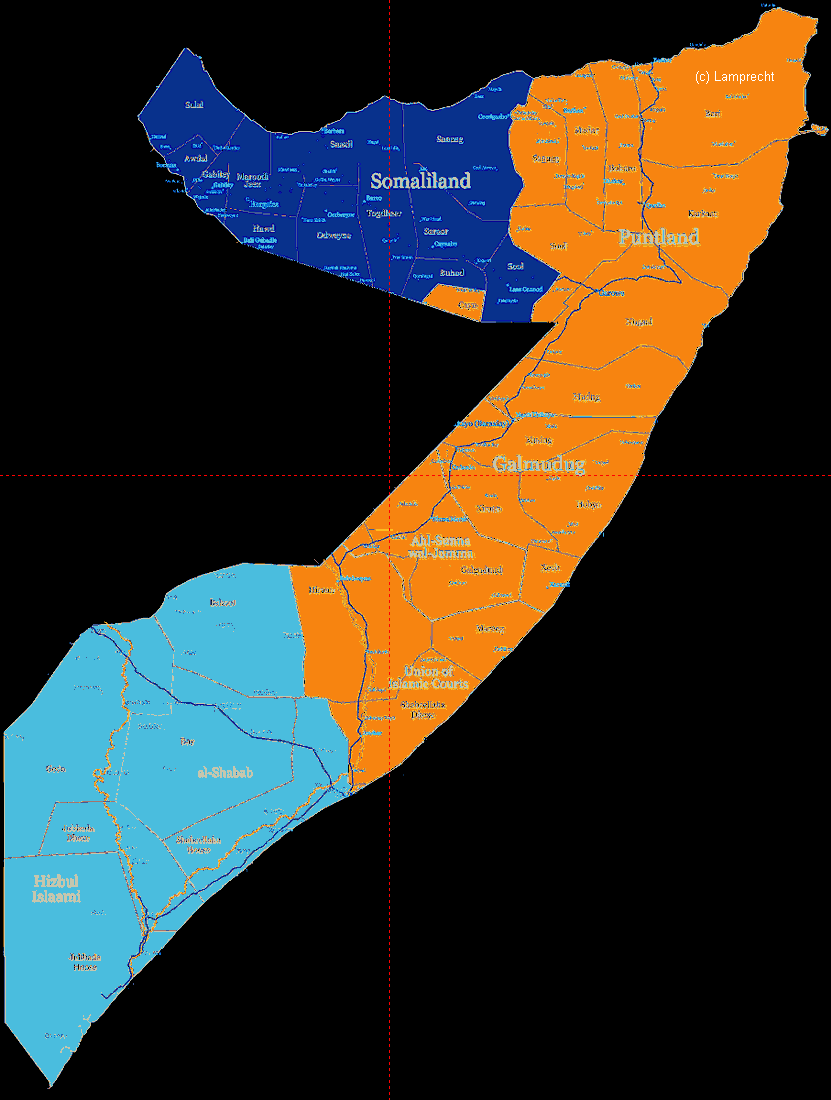
Bei Staaten wie Somalia liegt der Flächenmittelpunkt (geographischer Mittelpunkt) außerhalb des Landes (Äthiopien):

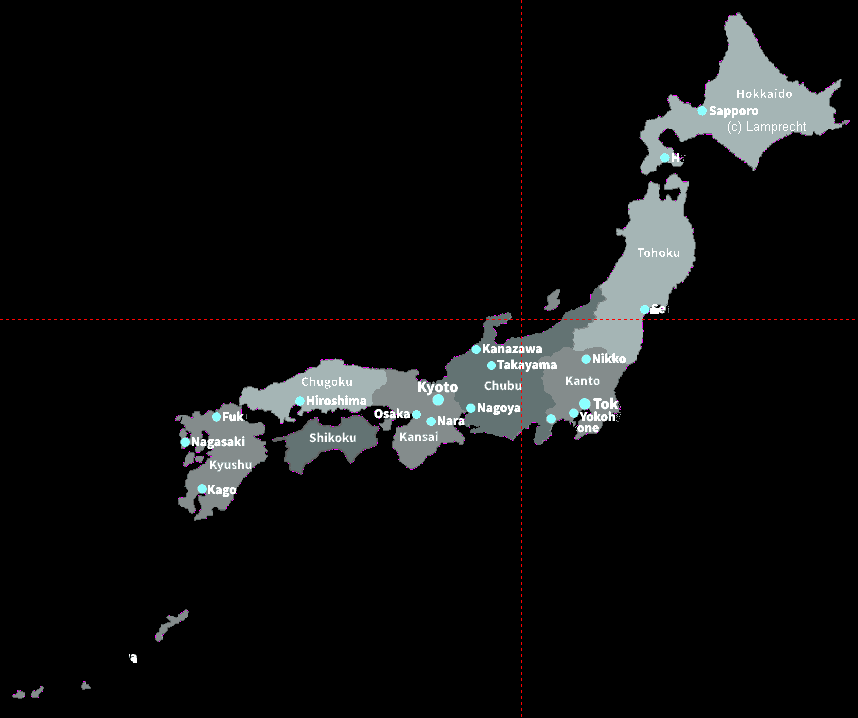
Bei Japan hatte ich leider keine genauere Vorlage:

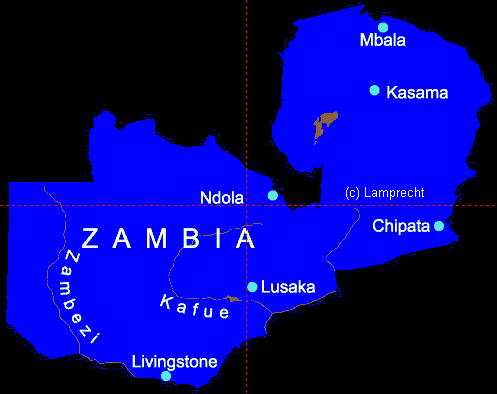
Sambia:

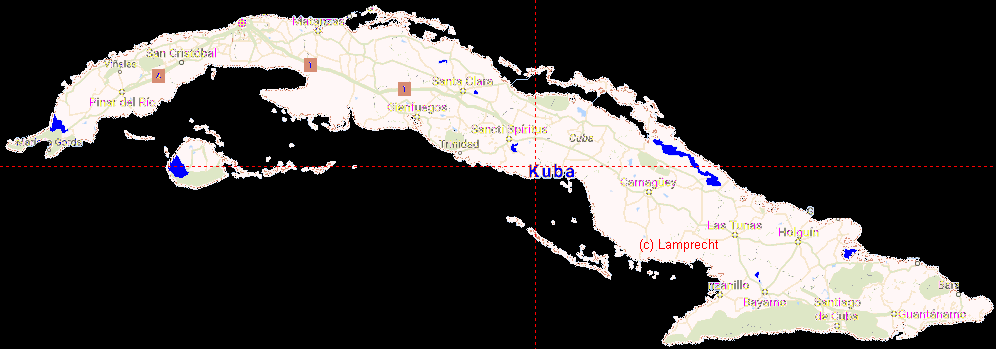
Kuba:

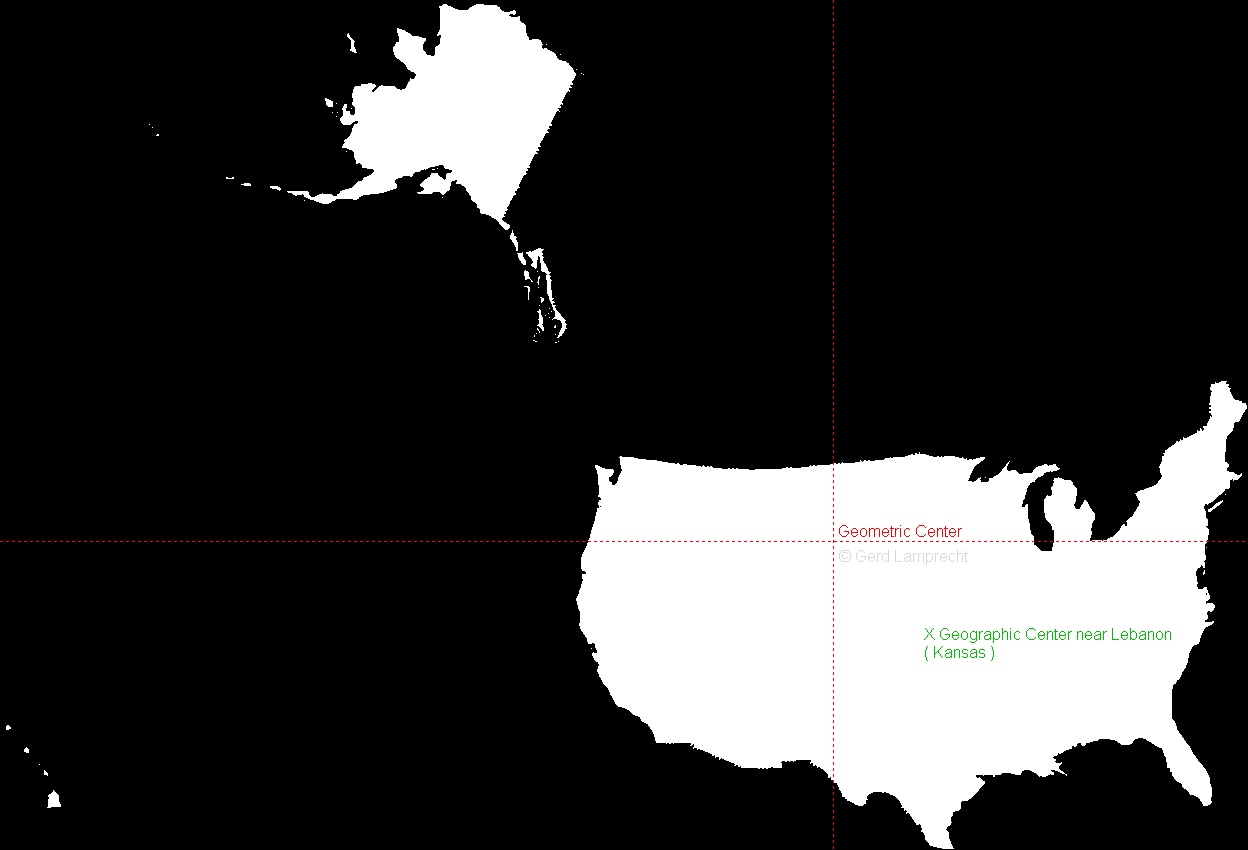
Geometrischer Mittelpunkt USA (Geometric Center of United States of America):

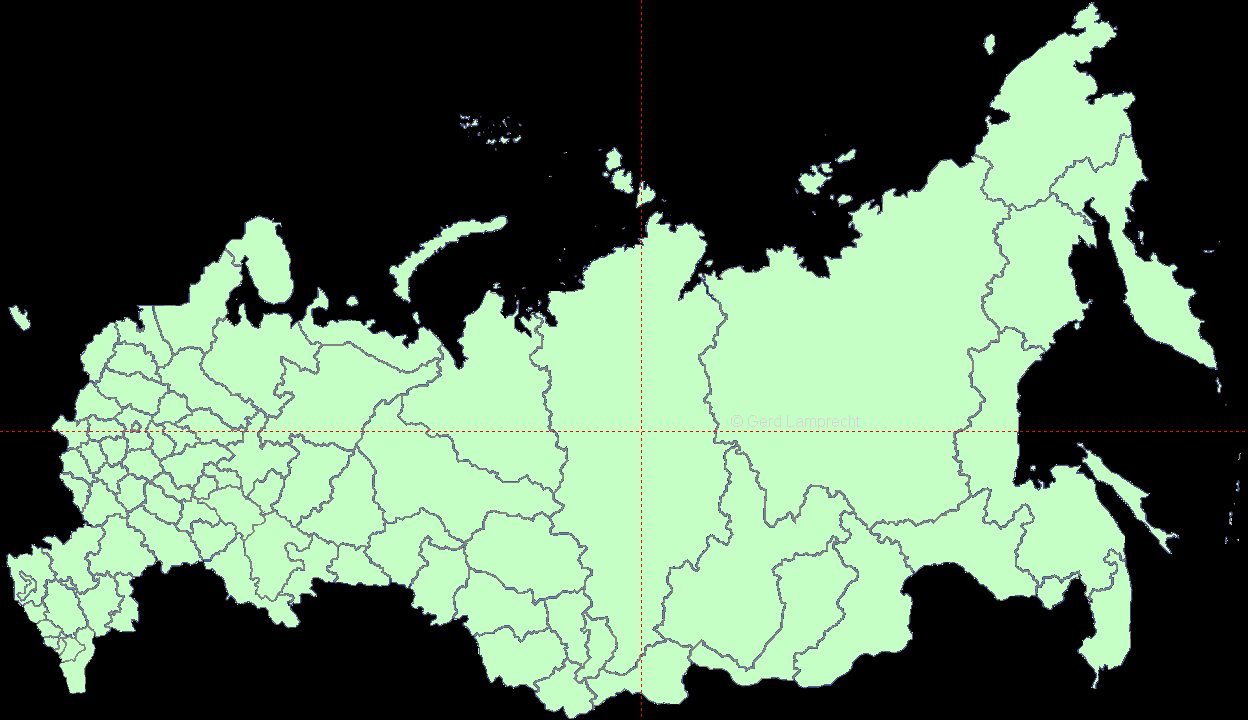
Geometrischer Mittelpunkt Russische Föderation (Geometric Center of Russian Federation):

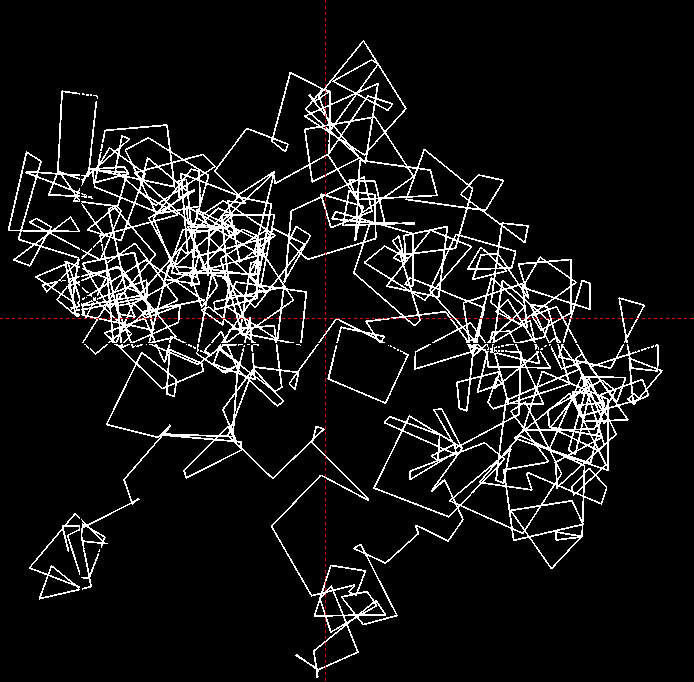
Bei Pi-Visualisierungen hat auch die Linienstärke Einfluß auf den geometrischen Mittelpunkt:

Selbst bei Textdokumenten kann man einen geometrischen Mittelpunkt bestimmen (Verschlüsselung):

Voynich-Manuskript S. 78 negiert, berechnet und verkleinert:

Mittelwert eines 2D Fraktals:

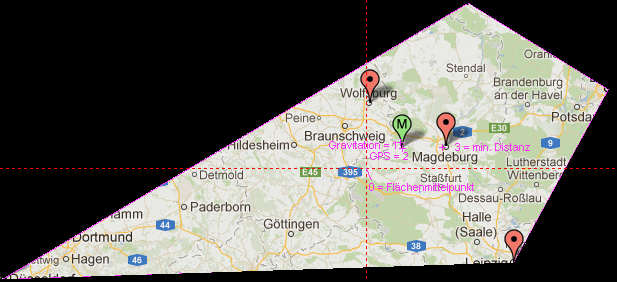
Vergleich Entfernungsminimum (Beispiel 6 Orte):

0 = Flächenmittelpunkt (der Entfernteste aus Düsseldorf bekommt höchste Wichtung; Nachteil: Orte innerhalb der Fläche ohne Wichtung)
1 = Gravitations-Mittelpunkt (durch 1/r² bekommt der Entfernteste geringste Wichtung; optimal für Wolfsburg)
2 = Durchschnitt GPS Koordinaten
3 = minimale Distanz (min Summe aller Entfernungen; optimal für Magdeburg und Berlin)
aus geomidpoint

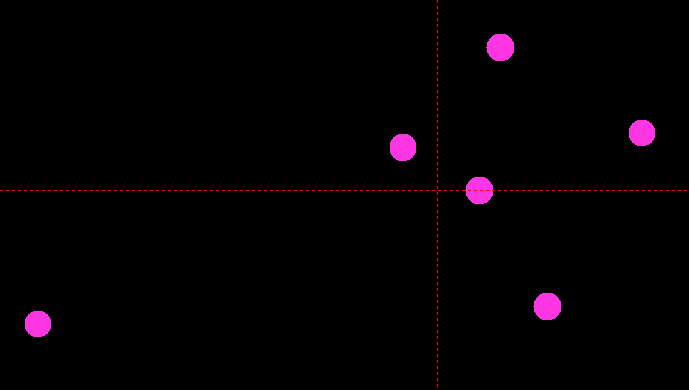
Berechnung des Gravitations-Mittelpunktes (obere Bild Punkt 1) per Kreisfläche:

Beispiel 1 Japaner und 8 Australier:

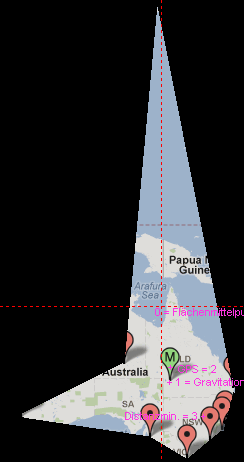
Nur mit "0 = Flächenmittelpunkt" ergibt sich ein Zentrum außerhalb vom australischen Festland.
Die "3=minimale Distanz" hingegen berücksichtigt nur die vielen eng beieinander liegenden Orte. Weit entfernte Einzelgänger haben hier Nachteile.

Interessant: http://de.wikipedia.org/wiki/K%C3%BCstenl%C3%A4nge
Inselstaat Malediven hat 2161 Meter Küstenlänge pro km²!
Hier spielt die Exaktheit der Karte eine große Rolle: links grob und rechts fein

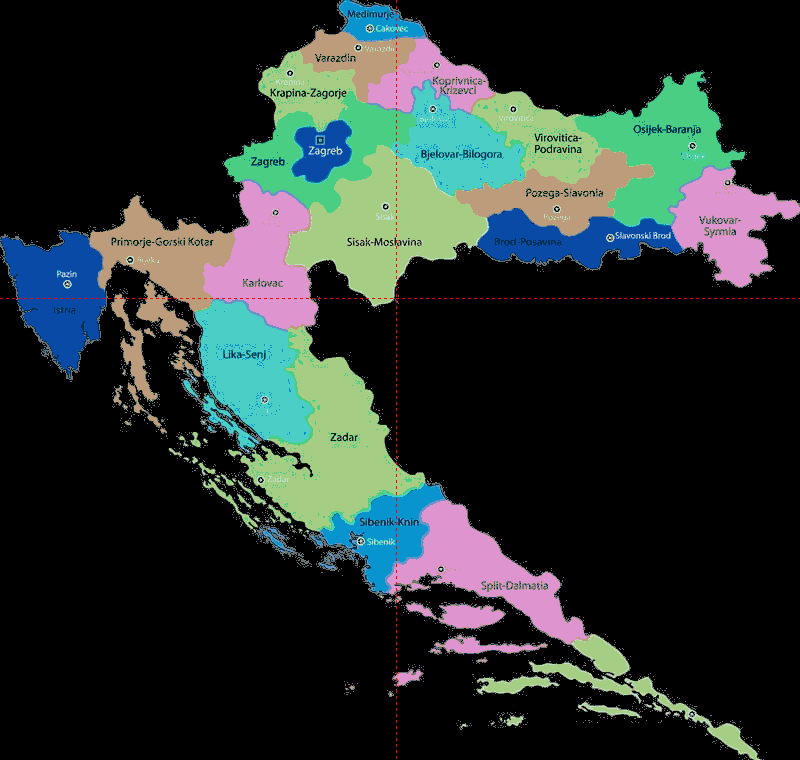
Kroatien:

Interessante Vorschläge einfach an (Interesting suggestions to): Kontakt