| Funktion / Function
|
Eingabe/Input
|
| Laufvariable i zum Erzeugen der Tabelle darunter; beginnt immer bei 0 und wird pro Schritt inkrementiert
|
i
|
Inkrementierungs Modus für die Laufvariable i und die Abbruchbedingung
IM=0 (oder keine Angabe): erst i++ dann Abbruchbedingung;
IM=1 erst Abbruchbedingung (z.B. für aB[i]) dann i++;
IM=2 erst Abbruchfrage, dann i++ nur, wenn kein Abbruch
|
IM
|
| TXTIN lokale Variable zum Lesen oder Beschreiben des Textfeldes oben rechts
|
TXTIN
|
| Liest vom Feld TXTIN ab der Pos0 Anzahl Zeichen; TXTIN.substr(Pos0,Anzahl)
|
GetTXTI(Pos0,Anzahl)
|
| Liest von strIn ab der Pos0 Anzahl Zeichen
|
strIn.substr(Pos0,Anzahl)
|
| UVT lokale Variable zum Lesen oder Beschreiben des unverschlüsselten Textfeldes unten vom Textkonverter Beispiele 63, 83
|
UVT
|
| IT lokale Variable, die nach dem Befehl Iter() die Anzahlder Schritte/Tiefe angibt
|
IT
|
| RT lokale Variable, die nach dem Befehl Reku() die Anzahlder RekursionsTiefe angibt
|
RT
|
| a,b,c,d lokale Variablen; werden unten angezeigt
|
a,b,c,d
|
| aB, aC, aD globale Feldvariablen (Arrays) zum Füllen der Tabelle; aB.length bestimmt Anzahl Zeilen
|
aB[0], aC[0], aD[0]
|
| Variable.length bestimmt Anzahl der Elemente (Feldgröße oder Anzahl der Textzeichen)
|
aB.length oder TXTIN.length
|
| Feld Fx erlaubt die Eingabe einer (Unter-)Funktion mit dem Argument (Übergabeparameter) x
|
Fx(x)
|
| Feld Fxy erlaubt die Eingabe einer Funktion mit den Argumenten (Übergabeparametern) x,y
|
Fxy(x,y)
|
| Feld Fx5 erlaubt die Eingabe einer Funktion mit den Argumenten (Übergabeparametern) x1,...,x5
|
Fx5(x1,x2,x3,x4,x5)
|
| e (Euler's number)
|
E
|
| Pi
|
PI
|
| phi=sqrt(5)/2+1/2 (golden ratio)
|
PHI
|
| ld(e)=log(E)/log(2)
|
LOG2E
|
| lg(e)=log(E)/log(10)
|
LOG10E
|
| ln(10)=log(10)
|
LN10
|
| ln(2)=log(2)
|
LN2
|
| Addition (egal ob Zahlen oder Strings)
|
+
|
| Subtraction
|
-
|
| Multiplication
|
*
|
| Division
|
/
|
| x Modulo y = Divisionsrest von x/y
|
x % y
|
| x XOR y bitweises exklusives ODER
|
x ^ y
|
| bitweises Schieben nach links
|
<<
|
| bitweises Schieben nach rechts
|
>>
|
| bitweises ODER
|
|
|
| bitweises UND
|
&
|
| logisches ODER
|
||
|
| logisches UND
|
&&
|
| logische Negation einer Variablen
|
!Variable
|
| Variable ungleich Variable ergibt Ergebnis vom Typ Bool (true oder false)
|
!=
|
| Potenzfunktion (Exponentiation); a hoch b
|
pow(a,b)
|
| natürliche Exponentialfunktion e hoch x
|
exp(x) oder pow(E,x)
|
| natürlicher Logarithmus ( zur Basis e)
|
log( )
|
| Fakultät (Factorial) x!
|
Fak( )
|
| Gamma(x) Gammafunktion
|
Fak(x-1)
|
| Absolute value; Betragsfunktion |x|
|
abs( )
|
| Vorzeichenfunktion Sign
|
sgn( )
|
| Quadratwurzel (Square root) x hoch 0.5
|
sqrt( )
|
| 3. Wurzel (Cubic root) cbrt(x)=x hoch (1/3)
|
pow(x,1/3)
|
| n. Wurzel von x (The nth root of x)
|
pow(x,1/n)
|
| reeller Zufallswert (Random number between 0 and 1)
|
random( )
|
| Logarithm of x to base b
|
log(x)/log(b)
|
| Cosine
|
cos( )
|
| Sine
|
sin( )
|
| Tangent
|
tan( )
|
| Secant(x)=1/cos(x)
|
sec()
|
| Cosecant(x)=1/sin(x)
|
csc()
|
| Cotangent
|
cot()
|
| Arc cosine
|
acos( )
|
| Arc sine
|
asin( )
|
| Arc tangent (returns answer between -Pi/2 and Pi/2)
|
atan( )
|
| Arc tangent (returns answer between -Pi and Pi)
|
atan2(y, x)
|
| Arc Cotangent
|
acot( )
|
| Hyperbolic cosine
|
cosh( )
|
| Hyperbolic sine
|
sinh( )
|
| Hyperbolic tangent
|
tanh( )
|
| Hyperbolic secant
|
sech( )
|
| Hyperbolic cosecant 1/sinh(x)
|
csch( )
|
| Hyperbolic cotangent
|
coth( )
|
| Antihyperbolic cosine
|
arcosh( )
|
| Antihyperbolic sine
|
arsinh( )
|
| Antihyperbolic tangent
|
artanh( )
|
| abrunden (Greatest integer less than or equal)
|
floor( )
|
| aufrunden (Least integer greater than or equal)
|
ceil( )
|
| Round (auf ganze Zahl runden)
|
round( )
|
| erf(x) Gaussian Error Function
|
erf(x)
|
| inverse erf
|
aerf(x)
|
| Binomialkoeffizient
|
Binom(oben,unten)
|
| BesselJ-Funktion
|
Bessel(x,y)
|
| Euler Polynome Beispiel 37; n ganzzahlig
|
EulerX(n,x)
|
| Stirling Number of the first kind
genauer und größer hier
|
StirlingS1(n,m)
|
| Stirling Number of the second kind
genauer und größer hier
|
StirlingS2(n,m)
|
| PrimzahlTest: liefert nur true zurück, wenn Argument (Parameter) eine Primzahl ist
|
IsPrim(x)
|
| liefert die x. Primzahl; Prime(1) ergibt 2, da sie die erste Primzahl ist; max=1230
|
Prime(x)
|
| kleinste gemeinsame Vielfache { lcm }
|
kgV(z,x)
|
| größter gemeinsame Teiler { gcd }
|
ggT(xa,xb)
|
| Quersumme { Digit sum } Integer oder String
|
QuerSum( )
|
Fresnel-sin-Integral
Mod=0 http://www.hp-gramatke.de/math/german/page0200.htm; WolframAlpha
Mod=1 sind die C1- und S1-Funktionen von Meek/Walton
Mod=2 also FresS(x,2)=FresS(x/sqrt(PI/2),0)*sqrt(PI/2)
Mod>2 sind Näherungsformeln "Wenn Kepler einen Computer gehabt hätte"
|
FresS(x,Mod)
|
| Fresnel-cos-Integral
|
FresC(x,Mod)
|
| Wandlung String in Dezimale Zahl (Integer)
|
Number( )
|
| Variable vom Typ Integer oder double in String wandeln; ohne Parameter wird es normale Dezimalzahl
|
Variable.toString(Basis)
|
| wandelt eine String-Zahl mit vorgegebener Basis in Dezimalzahl um
|
parseInt(strZahl,Basis)
|
| wandelt den dezimalen ASCII-Code in ein ASCII-Zeichen; String.fromCharCode(65)='A'
|
String.fromCharCode(lASCIIcode)
|
| wandelt das Zeichen an der Position Pos0 in dezimalen ASCII-Code; 'AB'.charCodeAt(0)=65
|
strIn.charCodeAt(Pos0)
|
| IsValInArrayIndex überprüft, ob ein Wert ab einer Position (Index) im Feld enthalten ist; true oder false
|
IsValInArrayIndex(Wert, Feld, Index)
|
| numerische Bestimmung des Minimums einer Funktion in den Grenzen Beispiel 50
|
SuchMin(strFormel,xMin,xMax,yMin,yMax,strBedingung,genau)
|
| numerische Bestimmung des Maximums einer Funktion in den Grenzen Beispiel 50
|
SuchMax(strFormel,xMin,xMax,yMin,yMax,strBedingung,genau)
|
| Numerische Integration: die Genauigkeit (Abbruchgrenze=Differenz zum Idealwert) darf bei großen Zwischenwerten nicht zu klein sein,
da sonst die Gefahr der Endlosschleife besteht (Beispiel 29)
|
IntegralG(Start, End, strFormel(x),Genauigkeit)
|
| Numerische Ableitung (Differentiation) der Funktion Fx(x) an der Stelle b (Beispiel 32)
|
Ableitung1(b)
|
| Berechnung der Ziffernhäufigkeit im Text; Ergebnis wird in der 1. Feldvariable abgelegt; Parameter 3 bestimmt, ob relativ in % (1) else absolut (Beispiel 63)
|
an(aB,strIn [,1])
|
einfache Umschaltung beim Regula-falsi-Verfahren
nMod=0=Illinois; 1=Pegasus 2=Anderson-Björck (Beispiel 35)
|
Nsuch(nMod,F2,Fz)
|
| wandelt ein Datum vom Typ String in den Type Date um (Beispiel 55)
|
StrDatum2Date(strDatum)
|
| wandelt ein Datum vom Typ Date in die Anzahl der Tage (Beispiel 55; "01.01.0100 00:00:00" ergibt 36520)
|
Date2Tage(dDate)
|
| addiert zu einem Datum vom Typ Date eine Sekundenanzahl hinzu (Beispiel 55)
|
DateAddSek(dDate,intSekunden)
|
| Gibt von der Kreiszahl Pi ab der Position Pos eine vorgegebene Anzahl an Stellen als String zurück
|
GetPiDezi(Pos,Stellenanzahl)
|
Gibt von wichtigen OEIS-Konstanten ab der Position Pos eine vorgegebene Anzahl an Stellen als String zurück
meine eigenen Konstanten sind negativ Such-Datenbank
|
GetKoDezi(konstIndex,Pos0,AnzahlStellen)
|
| wandelt den in Fx stehenden String in reelle Gradzahl um; Parameter x bestimmt bei mehreren kommagetrennten Koordinaten die Position (Beispiel 52)
|
FxNachGrad(Index0)
|
Abstand 2er GPS-Koordinaten [°] siehe Beispiel 51; r=6378.388 [km]
Mod=0: Loxodrome-Gleichung (atan((l2-l1)/(log(tan(b2+Pi/4))-...)
Mod=1: Großkreisbogen=acos(sin(b1) * sin(b2) + cos(b1) * cos(b2) * cos(l2-l1))*r;
Mod=2: http://www.movable-type.co.uk/scripts/latlong-vincenty.html http://www.kowoma.de/gps/geo/mapdatum.htm
|
AbstandGPS(BrLat1°,Lon1°,BrLat2°,Lon2°,r, Mod)
|
Abstand 2er GPS-Koordinaten [°] siehe Beispiel 51; r=6378.388 [km]
Mod=0: direkte Linie
Mod=1: entlang der Kugeloberfläche mit Mittelpunkt=(0,0,0)
|
AbstandXYZ(xyz1,xyz2,Mod)
|
| AusmalAnzahl addiert die Wertigkeiten aller Ziffern der Zahl. Array(0,1,2,3,4,5,6,7,8,9) entspricht also der Quersumme der Zahl und Array(1,0,0,0,1,0,1,0,2,1) entspricht der Kindergarten-Funktion "zähle die ausmalbaren geschlossenen Flächen der Zahl"
|
AusmalAnzahl(Zahl, Array)
|
| FindKombination(Index0, Operator '*' oder '+', lErgebnis, Array aB) gibt alle möglichen Aufgaben aus, die mit den Zahlen im Array und dem Operator * oder + lErgebnis ergeben. Index0=0 bedeutet ab der ersten Zahl im Array beginnen
|
FindKombination(Index0, strOp '*' oder '+', lErgebnis, Array)
|
| hintere doppelte Zeichen löschen: KillHintere('11233','3') ergibt '112'
|
KillHintere(strIn,strZeichen)
|
| vordere doppelte Zeichen löschen: KillVordere('11233','1'); ergibt '233'
|
KillVordere(strIn,strZeichen)
|
Rotieren einer Zahl oder eines Strings um nAnzahl
Mod=0: rechts herum
Mod=1: links (left)
Mod=2: vertauschen
|
Rotier(Mod, nAnzahl, strZahl, optional Len)
|
bigc große Zahlen mit vielen Nachkommastellen als String berechnen
Mod=0: Addition, Mod=1: Subtraktion, Mod=2: Multiplikation, Mod=3: Division
Mod=4: pow floor, 5=Vergleich, 6=abs, 7=floor, 8=round, 9=Modulo, 10=sqrt
11=exp, 12=log, 13=Fak, 14=Fibonacci explizit, 15=sin, 16=cos, 17=atan, 18=pow reell,
19=agm, 20=IsPrime; die Zahl mit den meisten Nachkommastellen oder str2 bestimmt Ergebnis
Funktionen mit 1 Parameter(10,11,12,13...18) bestimmt 2. Parameter die Nachkommastellenzahl
|
bigc(Mod,str1,str2)
|
| erzeugt einen vorgegebenen String mit einer vorgegebenen Anzahl
|
addstr(String,Anzahl)
|
| Für bigc kann so ein String erzeugt werden, der die benötigte Nachkommastellenanzahl besitzt
|
MitGenau(strIn,lAnzahl)
|
Unter-Iteration z.B. für Doppelsummen mit internen Variablen x, i
Mod=0: while Schleife
Mod=1: do...while siehe Beispiel 61
strWhile: String mit boolschen Ergebnis; '(i< x)' bedeutet solange wie i kleiner x
strDo: String, was innerhalb der Iteration wiederholt berechnet werden soll
strRet: String, der den Inhalt der angegebenen Variable als Funktionsergebnis zurückgibt
|
Iter(Mod,x,i,strWhile,strDo,strRet)
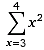
Iter(aB[0]=0,3,4,'x<=i','aB[0]+=pow(x,2);x++;','aB[0]')
|
Rekursionsfunktion; wenn in strBerechnung nochmals Reku auftaucht, kann der 3. Parameter
selbe lauten, um nicht nochmals alle 3 strParameter angeben zu müssen. Beispiel 17
|
Reku(z,x,strAbbrBedingung,strAbbrBerechnung,strBerechnung)
|
| erzeugt aus einer reellen Zahl einen strBruch
|
GetBruchNenner(dZahl,NennerMAX)
|
| ab einer Position gleiche Zeichen finden: GleicheLen('1311122',2)=3
|
GleicheLen(strIn,Pos0)
|
| ergibt true, sobald eine Ziffer ider ein Zeichen mindestens 2 mal vorkommen
|
IsZeichenDoppelt(ZahlOderString)
|
| überprüft, ob alle Ziffern (Zeichen) der 1. Zahl in der 2. Zahl enthalten sind; Reihenfolge egal
|
AllZiffernInZahl(Zahl1Ziffern,Zahl2)
|
| überprüft, an welcher Position das Muster in der Quelle enthalten ist; Werte kleiner als 0 bedeutet nicht enthalten
|
strQuelle.search(strMuster)
|
| nächste Zahl ohne doppelte Ziffern; NextNoDblZahl(45,12,5,54) ergibt 51, da nur Ziffern 1,2 bis 5 erlaubt; wäre MaxZahl=50, ergibt es 12 (wieder von vorn)
|
NextNoDblZahl(Zahl,vonZiffern,bisZiffer,MaxZahl)
|
| Fibonacci(x) Modulo y; mit GetPisanoPeriod(y) werden große Zwischenergebnisse vermieden
|
FibMod(x,y)
|