Gegeben seien die Seite a, die Höhe h und die Länge der Winkelhalbierenden w:

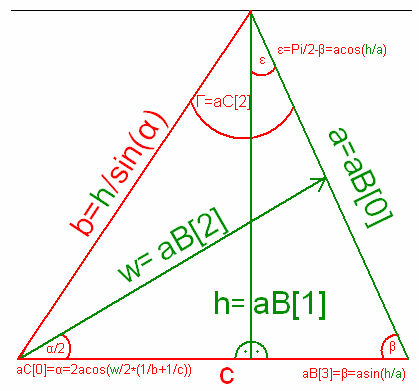
Über den Sinussatz gilt: c= a*sin(Pi-α-β)/sin(α);

b= h/sin(α); β =asin(h/a);

Für die Winkelhalbierende gilt: 2/w*cos(α /2)=1/b+1/c

Nun setzt man die ersten 3 Formeln in diese und stellt sie nach α um:

α = asin[h*(2/w*cos(α/2)-1/{a*sin(Pi- α -asin(h/a))/sin(α)}]

1. Diese Formel lässt sich leider nicht leicht nach einem α umstellen.

2. Diese Formel zeigt in Iterationen leider divergentes Verhalten.

3. Das Bisektionsverfahren ist ein möglicher Lösungsweg: man zieht α ab und sucht die Nullstelle.

Alle Lösungen gibt es bei meinem Iterationsrechner Beispiel 76.