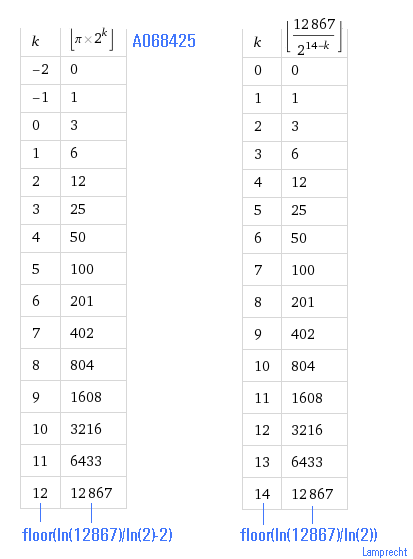
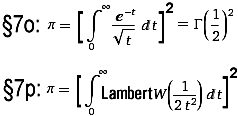Kreiszahl
Pi = π (Archimedes-Konstante oder Ludolphsche Zahl A000796=3.14159
zurück zu Gerd Lamprecht's Homepage
Auszüge der ersten 200000260 Stellen (Textkonverter)
Pi Nachkommastellen in Bildern visualisiert
1761...1768 Johann Heinrich Lambert: Beweis der Irrationalität von Pi per Kettenbruch
6 Beweise der Irrationalität von Pi bei Wikipedia
Die Kreiszahl-Konstante (auch Ludolphsche Zahl) wird ab 1706 mit dem griechischen Buchstaben π und ab 2001 in der Zahlen-Datenbank (OEIS) als A000796 bezeichnet.
Der griechische Buchstabe π kann verschieden dargestellt werden (auch Abhängig vom Browser):
| Bild | Unicode 03C0 mit Schrift Times New Roman | Windows Zeichentabelle | LaTeX-Syntax | HTML-Syntax | Unicode-HTML |
|---|---|---|---|---|---|
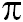 | π | U+03C0 | \pi | Π | Π |
Neben den allgemein
bekannten Definitionen und geschichtlichen Hintergründen wie z.B. in:
http://numbers.computation.free.fr/Constants/Pi/pi.html
http://de.wikipedia.org/wiki/Kreiszahl
http://dir.yahoo.com/Science/Mathematics/Numerical_Analysis/Numbers/Specific_Numbers/Pi/
gibt es noch viele andere Berechnungsmethoden für
die berühmteste aller mathematischen Konstanten.
Hinweise:
- Einige Formeln sind im
WMZ-Format gespeichert, um auch beim Ausdruck oder starken Vergrößerungen beste
Anzeigequalität beizubehalten.
(nennt man die Datei in ZIP
um, kann man eine WMF-Vektordatei entkomprimieren)
- Dieses Dokument wird ständig aktualisiert… (Stand 04.05.2016)
- Mein Geburtstag ist in Pi
z.B. ab Dezimal-Nachkommastelle 99999e99e7234 (erste Vorkommen
bereits bei Nachkommaziffern abcdecec, hfcfafhdddg) enthalten.
Interessante und schnell konvergierende Berechnungsmethoden (über 100 Algorithmen für Pi)
- Arctan-Reihen
Ausgehend von der bekannten Integral Formel für den viertel Kreis:
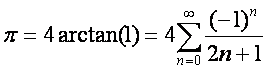 {Leibniz-Reihe (1646-1716)}
{Leibniz-Reihe (1646-1716)}
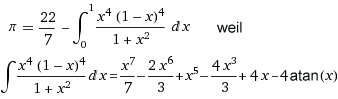
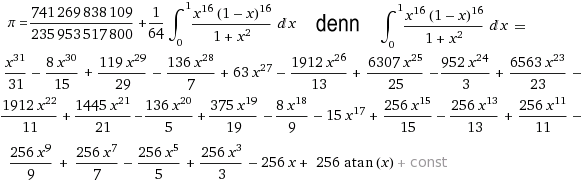
(bei Potenz 256 statt je 16 stimmt der Bruch vor dem Integral mit Pi auf etwa 156 Stellen überein)
und mit atan(1/Fibonacci(2x))=atan(1/Fibonacci(2x+1))+atan(1/Fibonacci(2x+2)) und
1er Summe: Pi=4*atan(1)
2er Summe:
Pi=(atan(1/2)+atan(1/3))*4 ; mit atan(1/x)=acot(x)
Pi=16*atan(1/5)-4*atan(1/239)
lassen sich viele besser
konvergierende Formeln herleiten (je kleiner der arctan-Parameter je schneller
die Konvergenz siehe http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpi.html
http://en.wikipedia.org/wiki/Machin-like_formula
http://www.machination.eclipse.co.uk/index.html
):
3er Summe:
Pi=atan(1/18)*48+atan(1/57)*32-atan(1/239)*20
http://numbers.computation.free.fr/Constants/Programs/piclassic.c
4er:
Pi=(3*23-1)*acot(23)+32acot(7*23+21)+20acot(23*157/2)+20acot(27091*23+5)
Pi=atan(1/57)*176+atan(1/239)*28-atan(1/682)*48+atan(1/12943)*96
5er:
Pi=508*atan(1/239)+752*atan(1/515)-480*atan(1/1068)+352*atan(2/81487)-576*atan(1/173932)
Pi=332*acot(107)+68*acot(1710)-88*acot(103697)-48*acot(2513489/2)-88*acot(18280007883/2)
Pi=352*acot(172)+204*acot(239)+128*acot(682)+176*acot(5357)+272*acot(12943)
6er:
Pi=(56acot[23]-acot[182]-25acot[500]-20acot[924]+5acot[99557]+10acot[298307])*4/3
Pi=732acot(239)+128acot(1023)-272acot(5832)+48acot(110443)-48acot(4841182)-400acot(6826318) (Hwang Chien-Lih 1997).
Pi=532acot(239)+728acot(1252)+928acot(2855)+400acot(58898)+248acot(110443)+552acot(4841182)
Pi=4(354acot[580]+227acot[1023]-171acot[1710]+310acot[5832]-12acot[2513489/2]+83acot[6826318])
Pi=1288acot(577)+304acot(682)+556acot(1393)+624acot(12943)+528acot(32807)+176acot(1049433)
7er:
Pi= 2324acot[1252]+3056acot[2855]+1064acot[5832]+1464acot[58898]+780acot[110443]+2148acot[4841182]+1064acot[6826318]
Pi=6348*acot(2852)+1180*acot(4193)+2372*acot(4246)+1436*acot(39307)+1924*acot(55603)+2500*acot(211050)-2832*acot(390112)
8er (ideal zum Parallelisieren {Multitasking, Multi-Processing} für 8 Kern Prozessoren {i7 = 4*2 oder AMD FX-9000-Serie}):
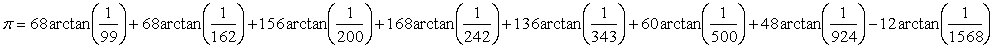
Pi = 13260acot[7535]+12888acot[9703]+4424acot[57532]-5284acot[167318]+1592acot[529661/2]-460acot[664373]+3436acot[1048768]-2500acot[7042807]
9er:
![]()
![]()

Pi=4(10958acot[39307]+18505acot[44179]+12000acot[167318]+1699acot[333367]+398acot[390112]-1369acot[2885139/2]+7162acot[3142271/2]+10118acot[1610057]+2475acot[103224943])
10er:
Pi=4(19162acot[40515]+12000acot[51412]+9000acot[219602]+11407acot[734557]+26463acot[1039784]-6271acot[6826318]-2988acot[7626068]-15764acot[9639557]+183acot[21072618]+8419acot[2539791558])
11er:
Pi=4(36462acot[390112]+135908acot[485298]+274509acot[683982]-39581acot[1984933]+178477acot[2478328]-114569acot[3449051]-146571acot[18975991]+61914acot[22709274]-69044acot[24208144]-89431acot[201229582]-43938acot[2189376182])
Dazu beginnt man z.B. im Intervall von 3 bis 4. Hier online per Iterationsrechner!
- Unendliche
Summen und Integrale
§2a: 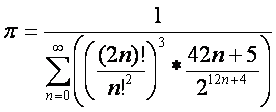 (Ramanujan)
(Ramanujan)
§2b: 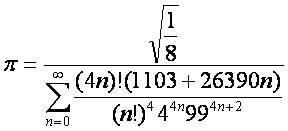 (Ramanujan; 8 Stellen pro
Term)
(Ramanujan; 8 Stellen pro
Term)
§2c: 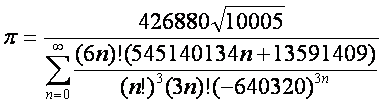 (Chudnovsky;
14 Stellen pro Term; Weltrekord 10 Bio Stellen!)
(Chudnovsky;
14 Stellen pro Term; Weltrekord 10 Bio Stellen!)
Hergeleitet aus hypergeometrischen Funktionen:
Pi=(51885171624116224000*sqrt(10005))/(1651969144908540723200*hyg3F2(1/6,1/2,5/6,1,1,-1/151931373056000)-30285563*hyg3F2(7/6,3/2,11/6,2,2,-1/151931373056000))
mit sehr nahe beieinander liegenden Konstanten:
0.999999999999999542922287559081630621837253677916255502...=hyg3F2(1/6,1/2...
0.999999999999999542922287559081630621837253677939777209...=(R-171)/(R-51)=1-120/(e^(sqrt(163)*Pi)-51)
0.999999999999994720752421307408525056714817085071348666...=hyg3F2(7/6,3/2...
0.999999999999994720752421307408525056714817076329642394...=(3R-1970)/(3R+2188)=1-4158/(2188+3e^(sqrt(163)*Pi))
und j(1+i*sqrt(163))=(-640320)³
z.B. https://gmplib.org/download/misc/gmp-chudnovsky.c
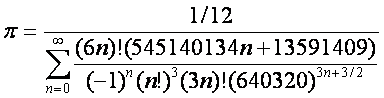 siehe Iterationsrechner Beispiel 72 bis 74
siehe Iterationsrechner Beispiel 72 bis 74
§2d: noch schneller konvergiert die Ramanujan–Sato-Reihe von J. & P. Borwein: 50 Stellen pro Iteration per Iterationsrechner Beispiel 88
§2e: 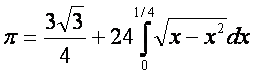
(Newtons Formel)
§2f:
Dazu ist auch das kürzeste c Programm bekannt: 138 Byte für 15000 Stellen:
§2g: Kettenbrüche:
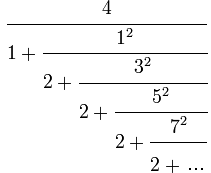 William Brouncker's Kettenbruch per Iterationsrechner Beispiel 98
William Brouncker's Kettenbruch per Iterationsrechner Beispiel 98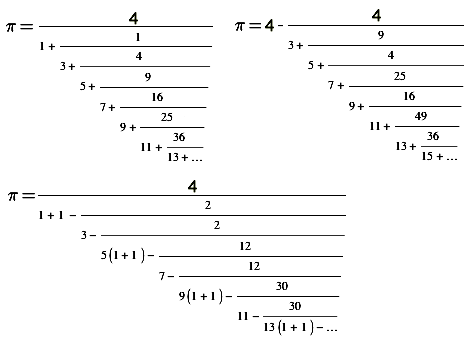
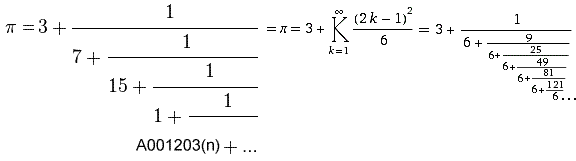
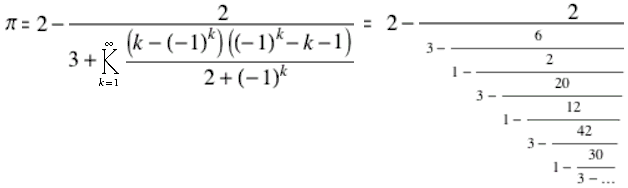
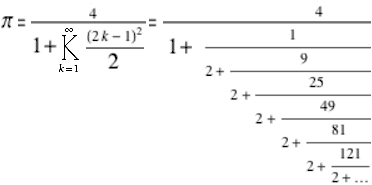
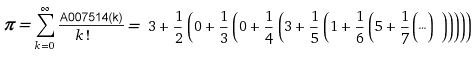
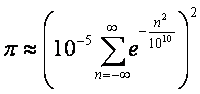 (Excessive
Fraud; correct to over 42 billion digits)
(Excessive
Fraud; correct to over 42 billion digits)
- Unendliche Produkte
§3a: Wallissches Produkt
§3b:
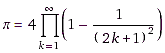 ;
;

§3c:
§3d:
§3e1:
§3e2: Pi=2/{Prod [1+(-1)^({Prime(k)-1}/2)/Prime(k)],k=2...∞}
§3f:
- Iterationen
§4a Iteration mit normaler Konvergenzgeschwindigkeit und Näherung von Archimedes von Syrakus über ein n-Eck per Iterationsrechner Beispiel 78
![]()
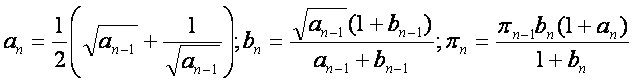
![]() (d.h. etwa N»1,9*2n Nachkommastellen; bei n=10 sind das
N»1995 Nachkommastellen)
(d.h. etwa N»1,9*2n Nachkommastellen; bei n=10 sind das
N»1995 Nachkommastellen)
bekannter
als Gauss-Legendre Algorithmus
(siehe http://de.wikipedia.org/wiki/Super_PI):

bei n=19 Iterationen sind
das etwa 1 Million Nachkommastellen.
§4d Noch besser
konvergiert die Iterationsformel von Borwein & Bailey (Konvergenz 5. Ordnung):
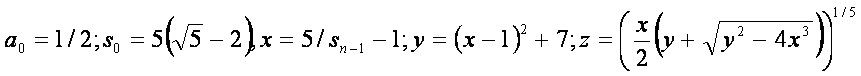
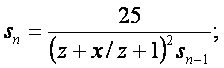
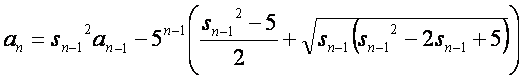
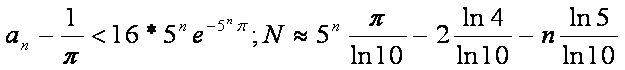
d.h. bei n=10 ergibt das
mindestens 13 Mio. Nachkommastellen!!!
siehe Iterationsrechner Beispiel 66
§4e Extreme Konvergenz mit Iterationsformel von Borwein & Bailey (Konvergenz 16. Ordnung):
per Iterationsrechner einfache Genauigkeit
1 Iteration 8 richtige Dezimalstellen; 2 I. 171 r. D.; 3 I. 2788 r. D.; 4 Iterationen ergeben über 10000 richtige Dezimalstellen! ...
Der krasse Gegensatz dazu ist einer der langsamsten Algorithmen zur Bestimmung von Pi:
§4f die Monte-Carlo-Simulation
-> benötigt 100000 bis 800000 Iterationen für 2 Nachkommastellensiehe Iterationsrechner Beispiel 10
Hintergrund ist die Frage, ob ein Zufallspunkt innerhalb eines Viertel Kreises liegt.
mathematisch: 1/N*sum (RandomReal[{0,1}]²+RandomReal[{0,1}]²)<=1,k=1...N mit N gegen UNENDLICH
Da das (Flächen-)Integral von sqrt(a²-x²) die bekannte asin-Funktion ergibt, läuft diese Frage auf die bekannte Formel hinaus:
Pi=2 * asin(1) eine Art numerischer Integration mit Umweg über Zufallsvariablen
Buffonsches Nadelproblem zeigt die gleiche Ineffizienz -> siehe Wiki...
Mit meinem PHP Rechner
für spezielle Umkehrfunktionen kann Pi auf vielfältige Weise berechnet
werden (z.B. wenn ein Taschenrechner keine Taste für Pi hat):
Pi = atan(1)*4
Pi = atan(1/sqrt(3))*6 =
Pi = acot(1)*4
Pi = asin(1)*2
Pi = asin(1/2)*6
Pi = asin(sqrt(5)/4-1/4)*10=asin(sqrt(2-sqrt(2))/2)*8=5asin(sqrt((5-sqrt(5))/8))=5acos((1+sqrt5)/4) usw. siehe sin(x) in Wurzelschreibweise
Pi = 29*asin(((-1)^(27/58)-(-1)^(31/58))/2)
Pi = acos(-1)
Pi = acos(0)*2=acos(1/2)*3
Pi = 2*(acos(1/x)+atan(1/sqrt(x*x-1))) mit |x|>1; bei x=13/5 ist Pi=(acos(5/13)+atan(5/12))*2=(atan(12/5)+atan(5/12))*2
Pi = Pochhammer(1,1/2)²*4=(4Pochhammer(1,3/2)/3)²=(8Pochhammer(1,5/2)/15)²=(16Pochhammer(1,7/2)/105)²
Pi = 4/binom(1,1/2)
Pi = sqrt(zeta(2)*6)
Pi = (zeta(4)*90)^(1/4)={Zeta(2*n)*(2*n)!*(-1)^(n+1)/(BernoulliB[2*n]*2^(2n-1))}^(1/(2n)) mit n=1,2,3,...
Pi = (Gamma(-1/2)/2)^2 = ((-3/2)!/2)² = Gamma(1/2)² = (-1/2)!²
Pi = (Fak(1/2)*2)^2 = (Gamma(3/2)*2)²
Pi = (Gamma(11/4)*4/(7/2)!!)^4
Pi = EllipticK(0)*2 = EllipticE(0)*2
Pi = (EllipticK(1/2)*Gamma(-1/4)²/8)^(2/3)
Pi = EllipticK(3/4)*2*agm(1/2,1)
Pi = EllipticK(1/10)*2/hyg2F1(1/2,1/2,1,1/10)
Pi = EllipticE(1/10)*2/hyg2F1(-1/2,1/2,1,1/10)
Pi = (5*EllipticK(-4)+3*EllipticE(-4))/3/hyg2F1(1/2,-1/2,2,-4)
Pi = (BesselK(3/2,1)*e)²/2
Pi = BesselK(1/3,2/3)/Ai(1)/sqrt(3)
Pi = 2/(BesselI(3/2,1)*e)²
Pi = 1/(BesselY(0,2)*BesselJ(1,2)-BesselY(1,2)*BesselJ(0,2))
Pi = 2*(Sin[1]/BesselJ[1/2,1])²
Pi = (sqrt(agm(1,sqrt(2)))*gamma(1/4))^(4/3)/2 = (agm(1,sqrt(2))*Gamma(1/4)²/sqrt(8))^(2/3)
Pi = (3*agm(1,(sqrt(3)-1)/sqrt(8))^(1/3)*gamma(1/3)/3^(3/4)/2^(4/9))^(3/2) = 3^(3/8)*agm(1,(sqrt(3)-1)/sqrt(8))^(1/2)*gamma(1/3)^(3/2)/2^(2/3)
Pi = Gamma(5/8)²*Gamma(7/8)²/(1/hyg2F1(1/4,3/4,1,1/2)²) = Gamma(5/8)²*Gamma(7/8)²/agm4(1,1/sqrt(2))
Pi =
(Gamma(1/6)(1/hyg2F1(1/3,2/3,1,1/2))/Gamma(2/3)/2)² = (Gamma(1/6)*agm3(1,
2^(-1/3))/Gamma(2/3)/2)²
Pi = sqrt((1/hyg2F1(1/3,2/3,1,1/2))/(2^(1/3)/(Gamma(1/3)³*3/4)))=sqrt(agm3(1,
2^(-1/3))*3/4*Gamma(1/3)³/2^(1/3))
Pi = (Dawson(1)*e*2/erfi(1))²
Pi = ((hyg1F1[-(1/2), 1/2,-1]-1/e)/erf(1))² = 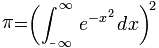 (aus gaußsche Fehlerintegral)
(aus gaußsche Fehlerintegral)
Pi = hyg2F1(1/2,1/2,3/2,1)*2=hyg2F1[1,1,3/2,1/2]*2=hyg2F1[1,1,3/2,1/4]*3*sqrt(3)/2
Pi = hyg2F1(0.5,1,1.5,-1)*4=hyg2F1(-1/2,1/2,3/2,1)*4=AppellF1[-1/2,1/2,1/100,3/2,1,0]*4=AppellF1[-1/2,-1/100,1/100+1/2,3/2,1,1]*4=AppellF1[-1/2,-1/100,1/100-1/2,3/2,1,1]*8/3
Pi = hyg2F1(5,-3/2,11/2,-1/3)*128/35/sqrt(3)=-hyg2F1[1,1,-1/2,1/4]*sqrt(3)*9/2
Pi = {hyg2F1[1,2,3/2,1/4]*2-4/3}*sqrt(3)*9/8=(hyg2F1[1/3,1,7/3,-1]*27/4+9-log(64))/2/sqrt(3)
Pi = -hyg2F1[-9/2,-7/2,-5/2,1]*4/63 = -AppellF1[-9/2,-7/2,1/100,-5/2,1,0]*4/63=-AppellF1[-9/2,-1/100,1/100-7/2,-5/2,1,1]*4/63
Pi = hyg2F1[1/2,2,3/2,-1]*8-2=(-hyg2F1[1,1,-1/2,1/2]-4)*2/3
Pi = 4hyg2F1(1,1/4,5/4,-1/4)+2acot(2)-log(5)
Pi = (2*hyg2F2[1/2,1/2,1/2,3/2,-1]/erf(1))²
Pi = (2*hyg2F2[-5/2,1,-5/2,3/2,1]/e/erf(1))²
Pi = 8*hyg2F3[{1/2,1},{3/4,5/4,3/2},1]/erf(sqrt(2))/erfi(sqrt(2))
Pi = [(sqrt(3) Gamma(1/3)^6)/(4 2^(2/3)*hyg3F2(1/2,1/2,1/2,1,1,1/4))]^(1/4)
Pi = [hygU(1/2,1/2,1/2)/(1-erf(1/sqrt(2)))]²/e
Pi = AppellF1(1/2,1/2,1/2,3/2,1,0)*2
Pi = AppellF1(-1/2,1/2,1/2,3/2,1,0)*4
Pi = AppellF1(1/2,1/2,1/2,3/2,1/2,0)*sqrt(8)
Pi = EllipticE(-1)/AppellF1(1/2,1/2,1,1,-1,-1)
Pi = AppellF2(1.5,0.5,1,1.5,2,0.25;0.5)*3/2
Pi = 12sqrt(3)-12-6AppellF2(0.5,-0.5,1,0.5,2,0.25;0.5)
Pi = sqrt((log(1/x)²/2+PolyLog(2,x)-(1/x-2)²/4 * AppellF3(1,1,1,1,3,2-1/x,2-1/x))*12) mit x=10000/19999:
Pi = sqrt((log(19999/10000)²/2+PolyLog(2,10000/19999)-(19999/10000-2)²/4 * AppellF3(1,1,1,1,3,1/10000,1/10000))*12)
Pi = -log(-1)*i = Im(log(-1)) = arg(-1+0i) = -2*atan2(0,-1) = -4*atan(-1) [durch Umstellung der Eulerschen Formel {Euler'sche Identität} e^(i*Pi)=-1]
Pi = 16/sqrt(27)/JacobiP(1/2,1/2,1/2,1/2)=sqrt(2/5)/JacobiP(1/2,-1/2,1/2,1/4)=2/JacobiP(1/2,-1/2,1/2,1)
Pi = ErdelyiG(1/2)=Digamma(3/4)-Digamma(1/4)=hyg2F1(1,1/2,3/2,-1)*4
Pi = PolyLog(1,2)*i=sqrt(PolyLog(2,1))*sqrt(6)=sqrt(6*PolyLog(2,1))=sqrt(-12*Polylog(2,-1))=sqrt(12PolyLog(2,½)+6log(2)²)=
=
Pi = Beta(1/2,1/2)=Gamma(1/2)²
Pi = -4*KelvinKei(0,0)
Pi = (Sin[A173201]-A173201*Cos[A173201])*2=A133731*sqrt(4-A133731²)-2*(A133731²-2)*acos(A133731/2)
Pi = Iter(1,0,3,'abs(i-x)>1e-16','x=i;i=i+8/(tan(i/4)+1)-4;','i'); (Konvergenz für Iterationsrechner)
Pi = 1/2*sqrt{3*sum (n!)³*(21n+13)/(2^(6n)*Pochhammer(3/2,n)³),n=0...inf}
Pi = 2*Si(∞)= Ci(-∞)/i = 2*Shi(i*∞)/i = 2*Chi(i*∞)/i 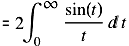
Pi = sqrt(sqrt(15)*sqrt(2783-4096*x)-105)/sqrt(10) mit x=(1536-5pi²(21+pi²))/3072 =
Pi = (3Gamma(1/3)*AGM(1,(sqrt(3)-1)/sqrt(8))^(1/3)/2^(4/9)/3^(3/4))^(3/2)=(3^(3/8)*sqrt(agm(1,(sqrt(3)-1)/(sqrt(8))))*Gamma(1/3)^(3/2))/2^(2/3)
5.1. Zusammenhang von Pi und Phi (golden ratio, Goldener Schnitt, Fibonacci)
[A01622]=Phi=Φ=Goldener Schnitt (engl. golden ratio)=(1 + sqrt(5))/2=1.61803398874989484820458683436563811772...
Fib(x)=Fibonacci(x)=(Φ^x - cos(Pi*x)/Φ^x)/sqrt(5)
§5.1.a:
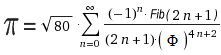
Pi = sqrt(80)*Sum[(-1)^n*Fibonacci(2n+1)/(2n+1)/[A01622]^(4n+2),{n,0,Infinity}] (bei n=74 stimmen 32 Stellen)
§5.1.b:
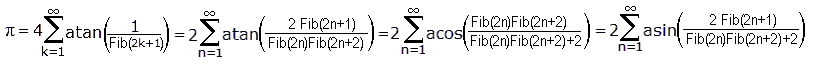
§5.1.c: aus sin(54°)=sin(Pi*3/10)=(1+sqrt(5))/4=Phi/2 folgt Phi=2*cos(Pi/5)=2*sin(3*Pi/10) und daraus folgt:
Pi = acos(Phi/2)*5=acos([(1+sqrt(5))/2]/2)*5 = acos((1 + e^(log(5)/2))/4)*5
Pi = asin(Phi/2)*10/3 = asin([(1+sqrt(5))/2]/2)*10/3 = asin((1+e^(log(5)/2))/4)*10/3
Pi = 10asin(Phi/2-1/2)=-10asin(1/4-sqrt(5)/4)
Pi = 5asin(sqrt(3-Phi)/2)=5asin(sqrt(5/2-sqrt(5)/2)/2)
Pi = asin(sqrt(2+Phi)/2)*5/2=asin(sqrt(5/2+sqrt(5)/2)/2)*5/2
Pi = asin(sqrt(1+Phi)/2)*10/3=asin(1/4+sqrt(5)/4)*10/3
5.2. Summen mit Binom(x,y)
Pi =
aus
Pi=
mit xs= 1/(2-sqrt(2+sqrt(2+sqrt(2)))) und w=sqrt(2+sqrt(2)) wird Pi =
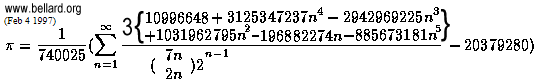
6. Grenzwerte wie Bruch-Funktionen, die gegen Pi konvergieren
§6a aus lim x! = lim sqrt(2Pix)*(x/e)^x folgt:
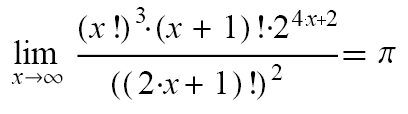 ein Bruch, der Pi im Unendlichen (also nie) erreicht!
ein Bruch, der Pi im Unendlichen (also nie) erreicht!
So stimmt x/y=226517876251716162692149071050771828410490449602080890536575346 / 72102879408277751642507260419334203501590758230297414247167791 mit Pi auf 86 Stellen überein!
§6b
per Iterationsrechner
§6c
§6d
§6e: Pi=lim ((2n)!!)²/(n((2n-1)!!)²),n-> inf = 2(Pi/2)^cos(2Pi*n) = Pi
§6f : Pi=[lim e^x*(x!)/(x^x*sqrt(2x)),x->inf]²
Per selbstkonvergierende Iteration (online) kann man solche Brüche (Näherungswerte) sehr schnell Pi annähern!
7. Berechnung einzelner Nachkommastellen (BBP) (online per Textkonverter):
D.H.
Bailey, P.B. Borwein and S. Plouffe, On the Rapid Computation of Various
Polylogarithmic Constants, Mathematics of Computation, (1997), vol. 66,
pp. 903-913
siehe http://numbers.computation.free.fr/Constants/Pi/piSeries.html#CITEPlouffe
siehe http://bellard.org/pi/ 2.7e12 Stellen!
siehe numberworld 1e13 Stellen!!!
Selbe Formel mit 5 verschiedenen html-Codes (6. WMZ wird von keinem neuen Browser mehr angezeigt):
§7a: Winword IE7 Symbol (veraltet):|
p = |
¥ |
|
æ |
4 8k + 1 |
- |
2 8k + 4 |
- |
1 8k + 5 |
- |
1 8k + 6 |
ö |
|
1 16k |
. |
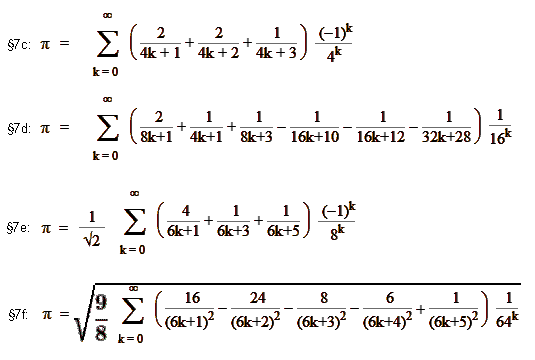
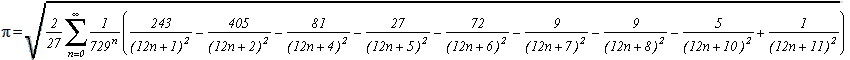
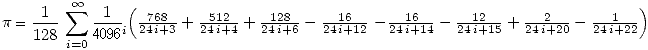 Iterationsrechner
Iterationsrechner


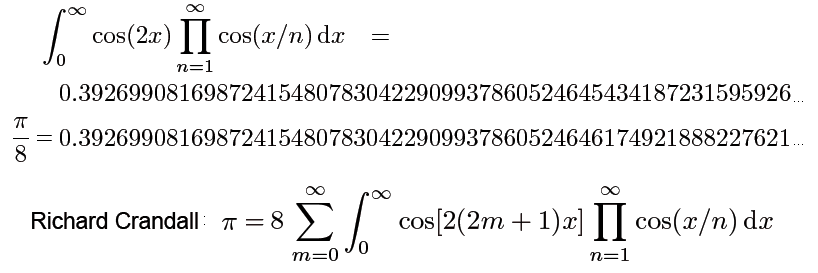
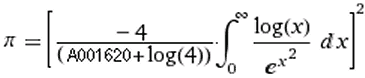
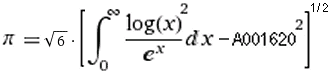
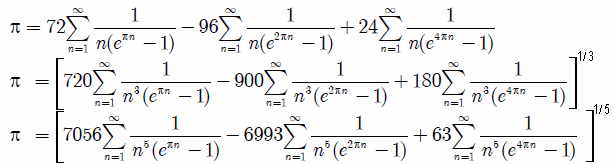
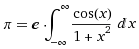
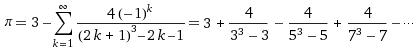 Nilakantha-Reihe 15. Jh.
Nilakantha-Reihe 15. Jh.