Primzahlen (Prime number; Sammlung interessanter Fakten)

Home...

1. Primzahlpolynome

Zunächst 4 unterschiedliche Quellen zu Primzahlpolynomen (alle unterschiedlich!):

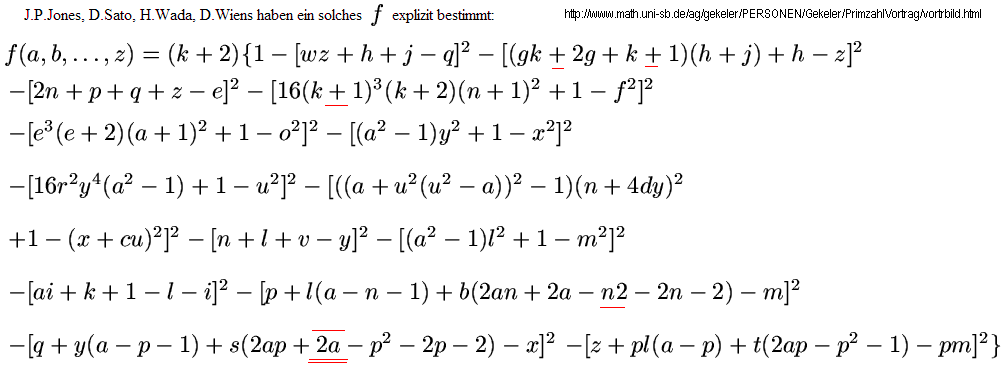
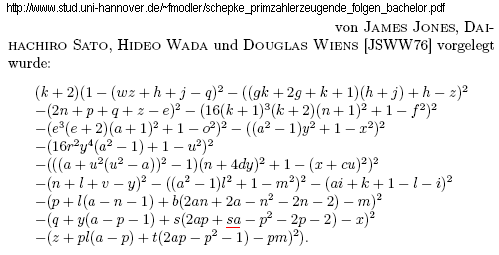
Link: http://www.aladin24.de/prim/index.htm

2. Primzahlerzeugende Folgen

· Jede Zahl testen: Iterationsrechner Beispiel 47 per Funktion IsPrime(x)

· Rekursion / Iteration aB[i+3]=aB[i]+aB[i+1];aC[i+1]=aB[i+1]/(i+1); siehe Übergabe an Iterationsrechner

Die 1 am Anfang von aD[0] ist absichtlich nicht „wegprogrammiert“, da nur einige Menschen die „2“ als erste Primzahl definierten.

· Folge mit ggT(x,y): Übergabe an Iterationsrechner

· Folge A202018 : Übergabe an Iterationsrechner (Polynom erzeugt 40 Primzahlen)

3. Primzahlzwillinge (Primzahlen Zwillinge engl. Twin Primes)

Zahlenpaar mit Eigenschaft: IsPrime(x) & IsPrime(x+2)

A001359 = A014574 - 1	A006512 = A014574 + 1
3	5
5	7
11	13
17	19
29	31
41	43
59	61
71	73
101	103
...	...
1260989	1260991
18409199	18409201
4999995017	4999995019
49999999999999998491	49999999999999998493
4999999999999999999999999999999999994819	4999999999999999999999999999999999994821
32656499591185747972776747396512425885838364422981	32656499591185747972776747396512425885838364422983
...	...
318032361 · 2^107001 - 1	318032361 · 2^107001 + 1
3756801695685 · 2^666669 - 1	3756801695685 · 2^666669 + 1

· Iterationsrechnerbeispiel 46: Iterationsrechner Beispiel 46

4. Große Primzahlen selbst ausrechnen

a) online (Anfang und Ende; mittlere Stellen bleiben unbekannt)

· 2^607-1: an Iterationsrechner übergeben

· 94550! - 1 = 1.3855410590400807467090325 e429389: an php Umkehrfunktionen Rechner übergeben

· 2^43112609 - 1 = 3.1647026933025592314345372 e12978188: an php Umkehrfunktionen Rechner übergeben (pow mit N=1000000000000)

· 2^57885161 - 1 = 5.81887266232246442175100212113 e17425169: 48. Mersenne-Primzahl

b) offline exakt alle Stellen einer Mersenne-Primzahl ausrechnen
Da die exakte Berechnung von grossen Zahlen über 9 Mio. Stellen extrem lange dauert, muss man schon einen optimierten Compiler einsetzen.
PureBasic erzeugt echten 64 Bit Maschinencode und optimierte Langzahlarithmetik gibt's kostenlos dazu (M44 in etwas über 40 min):

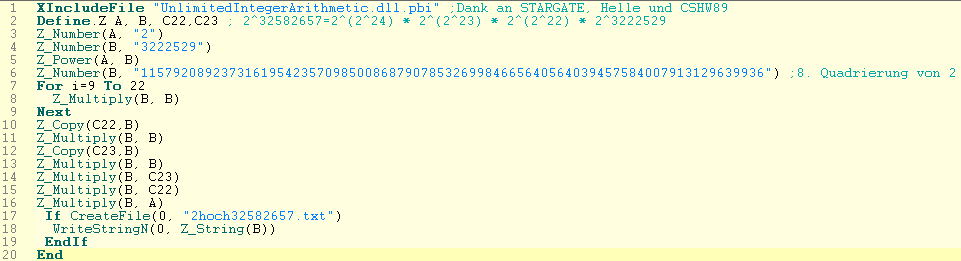
Ergebnisse:
M44_2hoch32582657-1 ; M45_2hoch37156667-1 ; M46_2hoch42643801-1 ; M47_2hoch43112609-1 ; M48_2Hoch57885161-1 ; M49_74207281 ; M50_M77232917-1.zip .

Neuer Weltrekord 07.01.2016 und neu 03.01.2018 M50: größte bekannte Primzahl aller Zeiten

primes.utm.edu 74207281
mersenne.org
2^74207281-1 = Mxx_2Hoch74207281-1.zip download
Aber das sind leicht zu testende Zahlentypen! Die 230 stellige RSA-230
ist bis heute nicht in ihre 2 Primfaktoren zerlegt!

5. Die Funktion Prime(x) und ihre Summendarstellung (erzeugt die x. Prinzahl)

Schon Euler entdeckte das nach ihm benannte Euler-Produkt (später durch Riemann präzisiert): Zeta(x)=
2 Sonderfälle beweisen die unendliche Anzahl der Primzahlen:
§5a: Grenzwert x -> 1: Die Divergenz der harmonischen Reihe (x-> unendlich für HarmonZahl(x)=Digamma(x+1)+A001620 und Zeta(1)=unendlich) führt zwangsläufig zum Schluß, daß das Produkt unendlich ist -> also muss es unendlich viele Primzahlen geben.
§5b: x=2: Zeta(2)= Pi²/6 = irrationale Zahl! Man kann nur mit unendlich vielen Bruch-Produkten eine irrationale Zahl erzeugen!
Später fand man eine exakte Formel zur Erzeugung der x. Primzahl:

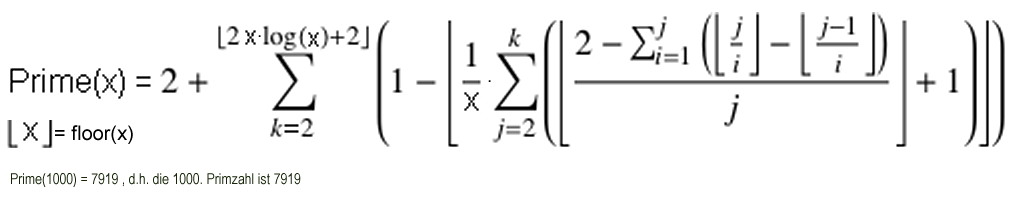
etwas schneller mit DivisorSigma[x]:

jedoch für große Argumente unbrauchbar.
Für größere Argumente online berechenbar unter Umkehrfunktionen Rechner 1. Komboboxeintrag
wobei für die Anzahl der Primzahlen bis k gilt:
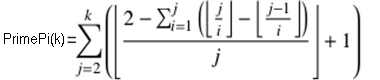 oder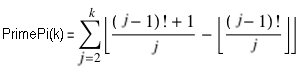
Als diese Formeln noch nicht bekannt waren, wurde die Zahl 1 fälschlicherweise per Definition in Meyers Konversations-Lexikon 4. Auflage 1890 mit zu den Primzahlen gerechnet:

Später wurde mit der Formeln von Mertens die Summe der Primzahlenkehrwerte verfeinert:

Mit der Zeit wurden immer bessere Approximationsformeln für große x gefunden:

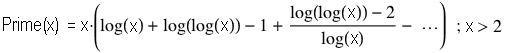
Damit und mit
n*(Log[n] + Log[Log[n]] - 1) < Prime[n] < n*(Log[n] + Log[Log[n]]) ; n > 5
kann man auch beweisen, dass die Lücken benachbarter Primzahlen unendlich groß werden können:
lim Prime(n+1)-Prime(n) =
lim ((n+1)*(Log[n+1] + Log[Log[n+1]] - 1 + (Log[Log[n+1]] - 2)/Log[n+1]))-(n (Log[n] + Log[Log[n]] - 1 + (Log[Log[n]] - 2)/Log[n]))
= UNENDLICH

6. Sophie Germain Primzahlen A005384 und A005385

Zahlenpaar mit Eigenschaft: IsPrime(x) & IsPrime(2x+1)

A005384=Sophie Germain Primzahlen	A005385
2	5
3	7
5	11
11	23
23	47
29	59
41	83
53	107
83	167
...	...
19391363	38782727
982452563	1964905127
100000000000000000000000000000007171	200000000000000000000000000000014343
999999999999999999999999999999999990221	1999999999999999999999999999999999980443
4999999999999999999999999999999999989539	9999999999999999999999999999999999979079
4999999999999999999999999999999999989821	9999999999999999999999999999999999979643
99999999999999999999999999999999999999999999965759	199999999999999999999999999999999999999999999931519
H.Dubner fand diese 727 Stellen 1999
...	...
3364553235 · 2^88888 - 1	(3364553235 · 2^88888 - 1)·2+1
18543637900515 · 2^666667 - 1	(18543637900515 · 2^666667 - 1)·2+1

7. Primzahldrilling (A022004 prime triples (p, p+2, p+6))

A022004	A022004 +2	A022004 +6
5	7	11
11	13	17
17	19	23
644051	644053	644057
1000000000000000000000000000000768841	1000000000000000000000000000000768843	1000000000000000000000000000000768847
...	...	...
81505264551807 · 2^33444 - 1	81505264551807 · 2^33444 +1	81505264551807 · 2^33444 +5

8. Primzahlvierling und Primzahlmehrlinge - Primzahltupel

show or download: List of smallest n-digit prime numbers (List of smallest n-digit prime k-tuplet)

  1er: Anzeigen smallest-n-digit-probable-prime.pdf worldofnumbers.com (& Norman Luhn)


 -1er: Anzeigen largest-n-digit-probable-prime.pdf worldofnumbers.com (& Norman Luhn)


  2er: Anzeigen smallest-n-digit-twin-primes.pdf Steffen Polster (& Norman Luhn)


  3er: Anzeigen smallest-n-digit-prime-triplets.pdf Norman Luhn (, Gerd Lamprecht)


  4er: Anzeigen smallest-n-digit-prime-quadruplets.pdf ; mehr Sucher & weitere Primzahlvierlinge


  4er Paare:Anzeigen smallest-n-digit-prime-quadruplet-pairs.pdf Norman Luhn


sexy prime quadruplet:Anzeigen smallest-n-digit-sexy-prime-quadruplet-pairs.pdf Norman Luhn


  5er: Anzeigen smallest-n-digit-prime-quintuplets.pdf Norman Luhn


  6er: Anzeigen smallest-n-digit-prime-sextuplets.pdf Norman Luhn , Gerd Lamprecht, Primentus


  7er: Anzeigen smallest-n-digit-prime-septuplets.pdf Norman Luhn , Gerd Lamprecht (20.10.2018)


  8er: Anzeigen smallest-n-digit-prime-octuplets.pdf Norman Luhn , Gerd Lamprecht, Horst_h


  9er: Anzeigen smallest-n-digit-prime-nonuplets.pdf Norman Luhn , Gerd Lamprecht, Horst_h


10er: Anzeigen smallest-n-digit-prime-decuplets.pdf Norman Luhn , Gerd Lamprecht


11er: Anzeigen smallest-n-digit-prime-11tuplets.pdf Norman Luhn , Gerd Lamprecht


12er: Anzeigen smallest-n-digit-prime-12tuplets.pdf Norman Luhn


13er: Anzeigen smallest-n-digit-prime-13tuplets.pdf Norman Luhn


14er: Anzeigen smallest-n-digit-prime-14tuplets.pdf Norman Luhn


15er: Anzeigen smallest-n-digit-prime-15tuplets.pdf Norman Luhn


10^x er: Anzeigen smallest-x100-digit-prime-k-tuplets.pdf Norman Luhn Status: 07.06.2021


5Digit: Anzeigen smallest-x5-digit-prime-k-tuplets.pdf Norman Luhn

Konstante Abstände von Primzahlen (AP mit... oder CPAP ohne andere Primzahlen dazwischen) siehe Jens Kruse Andersen's CPAP & Wiki's Primes in arithmetic progression

The largest known CPAP-6

Rank	Primes	n's	Digits	Year	Discoverer(s)
1	386140564676 · 1000# + 26861 + 30n (*)	n=0..5	427	2018	Gerd Lamprecht, Primo
2	44770344615 · 859# + 1204600427 + 30n	n=0..5	370	2003	Jens Kruse Andersen, Jim Fougeron, Primo
3	2121022995 · 859# + 1204600427 + 30n	n=0..5	369	2003	Jim Fougeron, VFYPR
4	200605912613 · 700# + 2437704499910036551539466113407 + 30n	n=0..5	301	2003	Torbjörn Alm & Jens Kruse Andersen, VFYPR

(*)

7564625198855140131650140547243491307536734300002412274412120410862007552117544125487358461576219935510887511629356987502217594095841510210118737219261032036591725016236599224151529914377234405413962533112523504185336077359036966916364339319601241892102799028686758337266120771495018761106322400455103916939500418089118724666335864751035216814963784444984844657588257604027017984324180061601738020589490297541353506016814382021

und 5 weitere im Abstand von 30.

The largest known CPAP-5

Rank	Primes	n's	Digits	Year	Discoverer(s)
1	2746496109133 · 3001# + 26891 + 30n	n=0..4	1290	2018	Norman Luhn, Gerd Lamprecht, APSieve, PrimeForm, Primo
2	406463527990 · 2801# + 1633050283 + 30n	n=0..4	1209	2013	David Broadhurst, PrimeForm, Primo
3	993530619517 · 2503# + 1633050253 + 30n	n=0..4	1073	2013	David Broadhurst, PrimeForm, Primo
4	495690450643 · 2503# + 1633050283 + 30n	n=0..4	1072	2013	David Broadhurst, PrimeForm, Primo
5	150822742857 · 2503# + 1633050253 + 30n	n=0..4	1072	2013	David Broadhurst, PrimeForm, Primo
6	94807777362 · 2503# + 1633050253 + 30n	n=0..4	1072	2013	David Broadhurst, PrimeForm, Primo
7	142661157626 · 2411# + 71427757 + 30n	n=0..4	1038	2002	Jim Fougeron, Primo

The largest known CPAP-4

Rank	Primes	n's	Digits	Year	Discoverer(s)
1	55072065656 · 7013# + 9843049 + 30n	n=0..3	3024	2018	Gerd Lamprecht, APSieve, Primo
2	62037039993 · 7001# + 7811555723 + 30n	n=0..3	3021	2013	David Broadhurst, PrimeForm, Primo
3	50946848056 · 7001# + 7811555723 + 30n	n=0..3	3021	2013	David Broadhurst, PrimeForm, Primo
4	26997933312 · 7001# + 7811555663 + 30n	n=0..3	3020	2013	David Broadhurst, PrimeForm, Primo
5	25506692100 · 7001# + 7811555693 + 30n	n=0..3	3020	2013	David Broadhurst, PrimeForm, Primo
6	198267970563 · 6007# + 7811555663 + 30n	n=0..3	2575	2013	David Broadhurst, PrimeForm, Primo
7	153104252515 · 6007# + 7811555663 + 30n	n=0..3	2575	2013	David Broadhurst, PrimeForm, Primo
8	60213811936 · 6007# + 7811555693 + 30n	n=0..3	2574	2013	David Broadhurst, PrimeForm, Primo
9	24576954772 · 6007# + 7811555723 + 30n	n=0..3	2574	2013	David Broadhurst, PrimeForm, Primo
10	25885133741 · 5003# + 3399421517 + 30n	n=0..3	2148	2012	Jim Fougeron, Primo
11	2^5900+ 469721931951 + 2880n	n=0..3	1777	2007	Ken Davis, NewPGen, PrimeForm, Primo

The largest known CPAP-3

Rank	Primes	n's	Digits	Year	Discoverer(s)
1	2683143625525 · 2^35176+ 1 + 6n	n=0..2	10602	2019	Gerd Lamprecht & Norman Luhn, APSieve, Primo
2	1213266377 · 2^35000- 1 + 2430n	n=0..2	10546	2014	David Broadhurst, PrimeForm, Primo
3	1043085905 · 2^35000- 18199 + 18198n	n=0..2	10546	2014	David Broadhurst, PrimeForm, Primo

The largest known sexy CPAP's ...

k	Primes	n's	Digits	Year	Discoverer(s)
3	2683143625525 · 2^35176+ 1 + 6n ; factordb ; Bild	n=0..2	10602	2019	Gerd Lamprecht & Norman Luhn, APSieve, Primo
3	18416522281203· 2^33222- 1 + 6n	n=0..2	10015	2020	Peter Kaiser, Primo
3	22582235875 · 2^22224 + 1 + 6n	n=0..2	6701	2019	Norman Luhn & Gerd Lamprecht,APSieve, Primo
3	(72865897 · 809857 · 4801# · (809857 · 4801# + 1) + 210) · (809857 · 4801# - 1) / 35 + 1 + 6n	n=0..2	6180	2019	Ken Davis, PrimeForm, APTreeSieve
3	20730011943 · 14221# + 344231 + 6n	n=0..2	6116	2019	Gerd Lamprecht, APSieve, pfgw
3	10409207693 · 2^20000 - 1 + 6n	n=0..2	6031	2019	Peter Kaiser
3	12909901425 · 12391# + 344237 + 6n	n=0..2	5320	2018	Gerd Lamprecht, APSieve, PrimeForm, Primo
3	(84055657369 · 205881 · 4001# · (205881 · 4001# + 1) + 210) · (205881 · 4001# - 1) / 35 + 1 + 6n	n=0..2	5132	2006	Ken Davis, PrimeForm, APTreeSieve
bestätigt von Jens Kruse Andersen
4	121152729080 · 7019#/1729+1 + 6n	n=0..3	3025	2019	Gerd Lamprecht & Norman Luhn, PrimeForm, Primo
4	1901870849 · (269504 · 1601# · (269504 · 1601# + 1) · (269504 · 1601# - 1) / 385) + 6 · (269504 · 1601# - 1) - 5 + 6n	n=0..3	2053	2019	Ken Davis, APTreeSieve, PrimeForm, Primo
4	46329193156 · 4657#+344231 + 6n	n=0..3	2001	2019	Gerd Lamprecht, PrimeForm, Primo
4	19299420002127 · 2^5050 + 17233 + 6n	n=0..3	1534	2019	Peter Kaiser, PrimeForm, Primo
4	1567237911 · 2677# + 3301 + 6n	n=0..3	1138	2019	Marek Hubal, PrimeForm, Primo
4	37675946750 · 2400# + 344231 + 6n	n=0..3	1034	2018	Gerd Lamprecht, APSieve, PrimeForm, Primo
4	2^3333 + 1582534968299 + 6n	n=0..3	1004	2010	Ken Davis, PrimeForm, Primo

Record history for the largest known AP-k (Primes in Arithmetic Progression) ...

k	Primes	n's	Digits	Year	Discoverer(s)
10	(3843864037 + 35500601·n)·691#+1	0..9	300	2019	Norman Luhn and Gerd Lamprecht
10	(3186700865 + 61959394·n)·653#+1	1..10	283	2010	Ken Davis, NewPGen, PrimeForm
10	(565429078 + 147743546·n)·641#+1	0..9	274	2009	Mike Oakes, NewPGen, PrimeForm
10	(1600616052 + 52323192·n)·617#+1	0..9	265	2009	Ken Davis, NewPGen, PrimeForm
10	(1079682357 + 109393276·n)·607#+1	0..9	260	2006	Mike Oakes, NewPGen, PrimeForm
10	(501788528 + 12970338·n)·463#+1	0..9	202	2005	Jens Kruse Andersen

Exotische Primzahlen (Prime Curious):

98635481221334*2999#+26861+30*n, n=0...4 ABER kein CPAP-5-Rekord, da 98635481221334*2999#+26863 auch PRIME!

A005478[14]=Fibonacci(A001605[14]=137)=19134702400093278081449423917
A005478[15]=Fibonacci(A001605[15]=359)=475420437734698220747368027166749382927701417016557193662268716376935476241

=32656499591185747972776747396512425885838364422981 (Primzahlzwilling aber keine Sophie Germain Primzahl)

9. Vorkommen und Anwendungen

- Informatik: http://de.wikipedia.org/wiki/RSA-Kryptosystem
- Informatik: gleichmäßige Belastung vieler Prozesse und Threads (Multitasking, Multiprocessing, PC, Server usw.) durch Taktrate=NextPrimeAfter(Taktrate) -> dadurch keine Aufschaukelung, da die Primzahl-Perioden nie Vielfache haben und so nie zeitgleich ablaufen
- Mathematik: Berechnung für Pi: Kreiszahl Berechnung per §3e
- Biologie: Fortpflanzungsrhythmus von Tieren =NextPrimeAfter(>4), damit sind Fressfeinde überfordert siehe http://de.wikipedia.org/wiki/Zikade#Fortpflanzung_und_Entwicklung
Was Zikaden mit Primzahlen zu tun haben
- Mechanik: Querschwingungen der Flügel werden bei N=NextPrimeAfter(N) weniger belastet (Laufrad einer 23-flügeligen Pelton-Turbine)
- Chemie: Es gibt in dem Zahlenbereich von 1 bis 83 der stabilen Ordnungszahlen und der beiden Lückenzahlen folgende Primzahlzwillinge: (5;7),(11;13),(17;19),(29;31), (41;43),(59;61),(71;73) http://www.primzahlen.de/primzahlen/chemie.pdf
- Astro- & SETI: http://de.wikipedia.org/wiki/SETI (bei Suche und Kontaktaufnahme spielen Primzahlen eine Rolle)
Vorkommen unter Vorbehalt (kann Zufall sein):
- Mathematik: in Alle n-stellige Zeichenketten garantiert in Pi zu finden: A036903≈10^n*(1.7+2.15*n)=43n*2^(n-2)*5^(n-1)+17*10^(n-1) -> 4 Primzahlen!
- (Prime(21)=73 Quasare = größte bisher entdeckte Struktur im Universum http://www.golem.de/news/astronomie-forscher-entdecken-unermesslich-grosse-struktur-im-all-1301-96932.html )
- http://www.astrobegleitung.de/Das_sonnensystem_als_organismus_primzahlen.html
- http://www.drillingsraum.de/room-forum/showthread.php?tid=1060
- Funktion PowPowMod() für Divisionsrest extrem großer Potenzen

Schnelle Prim-Algorithmen für große Zahlen:
1. http://en.wikipedia.org/wiki/General_number_field_sieve
2. http://de.wikipedia.org/wiki/Quadratisches_Sieb
3. http://en.wikipedia.org/wiki/Lenstra_elliptic_curve_factorization (Elliptic Curve Method)

10. Online Rechner Primfaktorzerlegung

- Funktion PrimfaktorenProdukt(x) (prime factorization 78 digits)
- Carmichael-Zahl-Faktorisierer (1000 digits)

50 Mio. Primzahlen:
http://primes.utm.edu/lists/small/millions/
Typen & Gruppierungen:
https://en.wikipedia.org/wiki/List_of_prime_numbers
http://mathworld.wolfram.com/TwinPrimes.html
http://mathworld.wolfram.com/PrimeTriplet.html
http://mathworld.wolfram.com/PrimeQuadruplet.html
http://mathworld.wolfram.com/PrimeConstellation.html
http://mathworld.wolfram.com/SexyPrimes.html
http://mathworld.wolfram.com/CousinPrimes.html
http://mathworld.wolfram.com/SophieGermainPrime.html
http://mathworld.wolfram.com/PrimeGaps.html (Lücken)

Primes in Arithmetic Progression (n Primzahlen mit gleichen Abständen)
wikipedia: Primes in Arithmetic Progression

andere Rekorde...