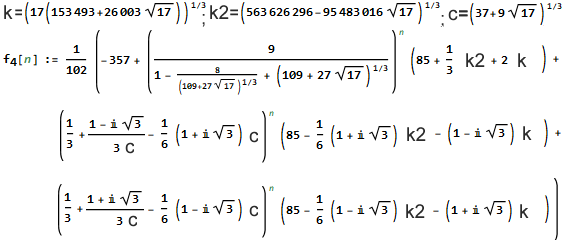
Roemisch_JAVA.htm##@NaB=Array(10,15,9);@N@Bi+3]=3*@Bi]-@Bi+1]+@Bi+2]+7;@Ni%3E11@N0@N0@N#...
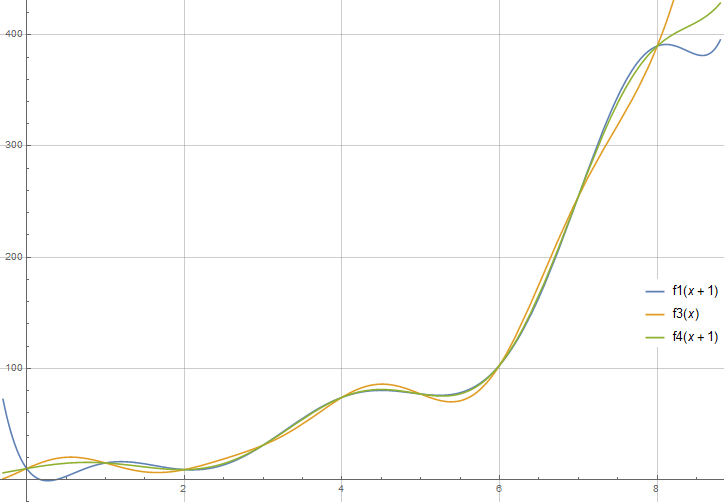
Algorithmen zur Zahlenfolge 10, 15, 9, 31, 74, 77, 103, 255, 390 |
| fn(x) | Typ | mathematische Beschreibung (Bildungsgesetz) | Link zum Nachrechnen | konkrete Terme (die Folge & deren Fortsetzung ) |
| 1 | https://de.wikipedia.org/wiki/Polynominterpolation | (x*(x*(21814456+x*(x*(3168368+x*(x*(30884+x*(622+x*(7*x-188)))-477029))-11256672))-21314208))/10080+807 | Roemisch_JAVA.htm#(x*(x*(21814456+x*(x*(3168368+x*(x*(30884+x*(622+x*(7*x-188)))... | 10,15,9,31,74,77,103,255,390,451,3249 |
| 2 | https://de.wikipedia.org/wiki/Kettenbruch | ContinuedFraction[(1398183330*Pi-728810)/(374473157+22741905*E),30] | https://www.wolframalpha.com/input/?i=ContinuedFraction%5B%281398183330*Pi-728810%29%2F%28374473157%2B22741905*E%29%2C30%5D | 10,15,9,31,74,77,103,255,390,451,21,1 |
| 3 | nichtlineare Regression mit nachträglicher Feinanpassung per trigonometrischer Interpolation | Fx(x)=0.215+1.268*cos(x*2)-1.71*sin(x*2)-4.185*cos(x*4)+11.683*sin(x*4)+10.6* cos(x*6)-13.6*sin(x*6)-7.499*cos(x*8)-5.6*sin(x*8); round(4.80114*exp(0.549627*i)+5.6-Fx(i*PI/9)) | Roemisch_JAVA.htm#0.215+1.268*cos(x*2... | 10,15,9,31,74,77,103,255,390,681,1177 |
| 4 | Rekursion, die auch in eine explizite Funktion gewandelt werden kann | Rekursion: a[n]=3*a[n-3]-a[n-2]+a[n-1]+7; & explizite Funktion: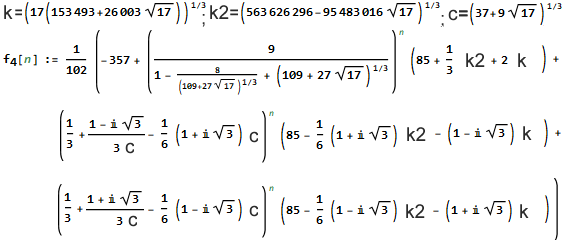
|
WolframAlpha: RecurrenceTable[{a[n]==3*a[n-3]-a[n-2]+a[n-1]+7,a[-2]==1,a[-1]==-1,a[0]==-1},a,{n,12}] Roemisch_JAVA.htm##@NaB=Array(10,15,9);@N@Bi+3]=3*@Bi]-@Bi+1]+@Bi+2]+7;@Ni%3E11@N0@N0@N#... |
10,15,9,31,74,77,103,255,390,451,833 |
| 5 | Nachkommastellen | (7578969 E)/1899398 - (3248188 Pi)/949699 | Roemisch_JAVA.htm##@Na=bigc(3,bigc(2,GetPiDezi(0,44),... | 10,15,09,31,74,77,103,255,390,477,707 |
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||