1. Zu jeder Zahlenfolge gibt es - wenn keine Einschränkungen getroffen werden - unendlich viele Lösungen.
2. Mit dem universellen Iterationsrechner kann fast jede Zahlenfolge online nachgerechnet werden.
Hinweis: JavaScript muss aktiviert sein. Per Lösungs-Link gelangt man auf die Seite des Iterationsrechners, wo man nur noch "Berechnung" klicken muss.
Tipp- oder Denkfehler, wie sie z.B. bei www.testedich.de Aufgabe 13 auftaucht, sind somit ausgeschlossen.
Einige Lösungen sind mit einem Passwort verschlüsselt.
Zunächst einfache Rekursionen und Polynome:
| XX,92,79,29,... |
mit Mittelwerte.html#92,79,29 hat man sofort die Interpolationspolynom Lösung und mit Fx(i-1) auch den Vorgänger
|
| 3,9,6,9,27,24,27 |
Lösung 1
|
| 9,27,8,24,11,33 |
Lösung 1 und
Polynomlösung 2
|
| 5,11,21,43,85,171 |
Lösung 1
|
| 1,2,6,42,1806,3263442 |
A007018 und
Polynomlösung 2
|
| 1,2,6,42,1806,2940042 |
Lösung mit String
|
| 27,29,54,62,108,128,216 |
Lösung 1
|
| 4,8,11,7,14,17,13,26 |
Lösung 1
|
| 8,11,9,4,25,441 |
Lösung 1 rekursiv und andere explizite Lösung
|
| 1,1,2,6,15,31,56,92 |
Iterationsrechner Beispiel 22 nicht A141126
|
| 75,75,100,150,240 |
Lösung 1
|
| 5,9,24,51,123,276 |
Lösungen 1 und 2
|
| 6,19,48,99,178,291 |
rekursive und Polynomlösung
|
| 1,6,21,56,126,252,462,792,1287 |
Lösung 1
|
| 189,270,27,81,18,27 |
Polynomlösung 1
|
| 189,270,27,81,18,21 |
Rekursionslösung und
Polynomlösung
|
| 3,4,8,14,23,44,68,134 |
Lösung 1
|
| 2,2,5,8,14,26,41,80 |
Lösung 1
|
| 32,42,58,123,171,279,585 |
%02%7Btx%05%042baflcve%7Dsb%10%15xk%13%15,f%7Cyetez%60umz%13%0A%08%16+igcdi~wdu%7Bwt%7D%0Ca%18%3E%7Fq%7D%60%7Fb%7Ftbmepvfaq0jfl~sxixifpdi%02%1DY%0D~oyt%60yaa%7Brz%02%04%3Cnz%08%0Bytdjazz%60%0F%08%11%00d%19%7F%0BY%09xoh%05%1A%0A%0D9%12%7B%17:%7C-kvac!%1Bn7;?%204g%06%12+%09my%0DoHu%7Bk%05%1A%7B%0E%1E%7F%06%1Fa
|
| 7,16,110,123,1091,2762,10309 |
%02%7Fm+obzxba%7Ffte%7Dry%16%17y%7Fgpy%0A%1E(ctxharrx%10%18%7Bi%60sda%0E%007jbk~urt%15%19%7B%7F%60jcx~%7D%0F%16)n%60mhx%13%17pw%60jcxe%10%1F%3E%7Dw%7Dnt%7B%14%19%7Fi%60sy%0A%1E(cpxh%60vpy%10%0Ey~cn%14%1A6%7Cxo%7Bsejuu%12%14%7Bwdqbz%7Daxs%11%0C%14%06r%10%1Ca%0Bv%0Ex%122f%60f%7D8%7Fe%7F%02%03ab!%1Bn%03,b'yt%06%13+%09y0%22TO,n%13%06=%17gk%0F%088%7Fi%7C%02%03%10a%06v%13%0Bw
|
| 7,16,110,123,1091,2762,33130 |
Lösung 1
|
| 1,2,2,7,17,167,3127 |
%02k%06%1D%05%16z%13m~%7D%11%00e%19%7F%7F%1AHuth%05%1A%0A%0C9%12%7By%02%16-o%7C%7C%0A%08%04:hf%17gz%0F%048of%19o%7C%1Aa%06/vv%11r%0E%1E~%06%1Fr%14%0Aa
|
| 2,5,7,11,29,199,4931 |
nicht aus Prim(0, 2, 3, 4, 9, 45, 657...) konstruiert: %02k%06%1D%05%16z%13prtj%02%16u%1Fp%14%1A!%7Ba~%14%04%0E%12&%1Blj%14%06+%60%10%7Ce%06%11,yx%13ye%06%13+yv%1Ff%10%1A%08%08:%60g%0Fw%10%01w%11%0Cd%04%0Cn
|
| ?,2,7,24,82,280,956,3264 |
rekursiv und explizit!
|
| 1,1,2,3,6,11,22,43,86,171 |
rekursiv und explizit!
|
| 5,5,4,7,9,5,-10,-41 |
§1 rekursive Lösung
|
| 5,5,4,7,9,5,7,68 |
§2 Polynom-Lösung1
|
| 5,5,4,7,9,5,6,61 |
§3 andere Polynomlösung
|
5,5,4,7,9,5,7,7,11,5,8 |
§4 Lösung
%7B%1Dep%05%1A%0A%0C%60%12%7Bdla%7F%02%0E%11%7Cus%7D%7Do%0A%00%10%0C/zs%09y0%22TO,f%7Bmag%0E%13&%1B%7C+%7Dns%7D%08%0Ehwc~%14%08'%7B~%1Bl0;1,)%01%09%60%06%11,%09a%0E%13&m%60%1F%7Dns%7D%08%0Eyvh%05%1A#kc%0A%7F%11%0Cd%04%0C%7Cao)t%17%1Ed%17swh%7Dq%16%0C%10%0B%03%1Ch%3C#!mef'%7C%7Fjv+qw%01pY%06da2w%10%11~%0Dd%7B%15%208v17jN%25+2m%14%08'%0Dfm%026&-,*%0FG:)%3E%06%3C+%3C%13%20%224b%7Cpvd%1AHc%7Bb~sfi1%7D%02%0Ar%09ckv%01Eu%0F%07~%7Be
|
| 5,5,4,7,9,5,7,71 |
§7 iterative Lösung mit Polynom 4. Grades
|
| 5,5,4,7,9,5,7,8,12 |
§8 rekursive Lösung mit floor()
|
| 5,5,4,7,9,5,1,6,2 |
§9 rekursive Lösung ohne floor()
|
| 5,5,4,7,9,5,6,4,4,5,8,4,6 |
§10 A141298(81)
|
5,5,4,7,9,5,4,10,0,2,1,2,5 |
§11 Lösung
%10pqg%7C%0E?(1#*ra%14%0A%02%0F%11%7Ch%7Bspo%0A%0Ca%12flba%7F%02%0F%13%7Cufg~%14%04%0E%12&mb%1Fid%02%0C%09a%0A/%0Eh%14%08'%7B~%1Bxhtupf%01%09%08%04:ne%17c%10%0D/zp%09mhm%16%08hcape%7Fu%10%01/tq%11vp%0Do%10%08%08c%05%1Ai
|
5,5,4,7,9,5,4,5,5,1,2,4,2,1,3,2,1 |
§12 Lösung
%12qvcu.?(1#*ra%14%0A%02%0F%11%7Cuff~%14%08%7F%0Drfdy%14%06p%10%1C%01%7C%7D%13%0B%14%08'%7B%7C%1Blb%14%11%02%0C%09a%0A/%0Eh%14%08'%7B~%1Bxhtupf%09a%0A/xt%09g%0E%12&mc%1F%7Ddhz%01%08f2%3C%16%208'%3E(nxl'(+.D%09xjbltcnko%06%1F+qw%07%7F%13a%06w%13%0Bd%0A%00so
|
5,5,4,7,9,5,3,2,1,1,9,7,5 |
§13 Lösung
%15%7Crfs%0E%1F%08%11%03%0Aqaw%04%0C%0Dc%11%15fnpo%0A%0Ca%12%7Bdy%14%06p%10%1C%01%7C%7D%13%0B%14%08'%7B%7C%1Bl%02%15l%02%0FH%7Ce%06%11,%7F%7B%13yef%60p%7Fl%02%0FH%0Ay%1B~%05%16#eb%12o%7Bbcmy%0DbH%15%7B%13%07=%17%60$%20%15%250=*%25e%01%08f5?,7/f%60cwqko%04%0C$%04%12%0Dta%05%1A%7B%0E%1E%7F%06%1Fatd
|
| 5,5,4,7,9,5,6,9,11 |
§15 andere Lösung
|
| 5,5,4,7,9,5,4,11,9 |
§16 andere Lösung
|
| 5,5,4,7,9,5,10,99 |
§17 andere Lösung
|
| 5,5,4,7,9,5,10,-1,-33 |
§18 kurze Iteration nur mit Grundrechenarten
|
| 5,5,4,7,9,5,0,-1,-3 |
§19 Iteration mit Grundrechenarten und Vorzeichenwechsel
|
| 5,5,4,7,9,5,8,7,17 |
§20 Iteration mit Grundrechenarten und Vorzeichenwechsel
|
| 5,5,4,7,9,5,7,4,9,9,9,8,2,7 |
§22 ein Bruch
|
| 5,5,4,7,9,5,11,4,5,10,4 |
§23 eine Wurzel
|
| 1694,1768,1576,1253,0727,0979,1697,1566,1152,0616 |
Polynomlösung
|
| 92,79,29,-58 |
Polynomlösung
|
| 92,79,29,8,82 |
Polynomlösung
|
2,10,4,7,6,9,5,1,3,8 |
exakte Polynomlösung statt der oft gewünschten Antwort "1-10 alphabetisch rückwärts sortiert"!
|
81,9,18,2,11 |
2 unterschiedliche Lösungen
|
| 4,18,30,37,75,84,92,1000,6250 |
eine mögliche Polynomlösung (auch die von Professor Eckbert München?)
|
| 8,3,1,11,5,9,6,7,4,10,2,12,7267 |
eine mögliche Polynomlösung (nicht die mit Buchstaben, die bei 12 endet!)
|
| 5,8,12,19,28,40,58,84 |
§A1 rekursive Lösung 1
|
| 5,8,12,19,28,35,33,12 |
§A2 Polynom-Lösung
|
| 5,8,12,19,28,41,57,78 |
§A3 andere rekursive Lösung
|
| 1,1,3,7,17,41,99,239,577,1393,3363,8119 |
A001333 rekursiv und explizit
|
| 16,17,256,257,272,273,4096,4097,5012,5013,14444 |
Lösung 1
|
| 3,4,8,17,33,58,94 |
A153057 explizit und iterativ auch A000330: 0,1,5,14,30,55,91,140,204
|
| 0,0,1,1,4,3,9,6,16,10,25,15,36,21,49,28,64,36 |
A123596 explizit und rekursiv
|
| 11,13,17,11,14,11,15 |
2 mögliche Lösungen
|
| 3,12,43,118,259 |
2 mögliche Lösungen auch A178073=1,10,41,116,265,526
|
| 1,9,26,219,755 |
mögliche Lösung
|
| 3,8,24,48,120 ,323 |
Polynom-Lösung §B1
|
| 3,8,24,48,120 ,168 |
mögliche Lösung §B2=A084920=Prime(x)²-1
|
| 3,8,24,48,120 ,195 |
Polynom-Lösung §B3
|
| 3,8,24,48,120 ,143 |
Polynom-Lösung §B4
|
| 3,8,24,48,120 ,224 |
Polynom-Lösung §B5
|
| 3,8,24,48,120 ,268 |
Polynom-Lösung §B6
|
| 3,8,24,48,120 ,534 |
2 Nachkomma-Lösungen §B7 +§B8 3.008 024 048 120 534 366 419... und 3.008 024 048 120 534 366...
|
| 3,8,24,48,120 ,519 |
§B9 Suche in Pi Nachkommastellendatenbank nach Ziffernfolge 382448120 ergibt die Nachkommastellenposition i=200691468 (NK=3 8 24 48 120 519...)
|
| 3,8,24,48,120 ,168 |
kgV-Lösung §B10 (vergl. A075059)
|
| 3,8,24,48,120 ,168,168 |
§B11: rekursive Produktfolge mit A007068/!x
|
| 3,8,24,48,120 ,168 |
§B12: rekursive Produktfolge mit Polynom3/!x
|
| 12,8,5,3,2,2 |
3 Algorithmen: explizit, rekursiv, Mod auch 12,8,5,3,2,2,3,5,8,12,17,7,...
|
| 12,8,5,3,3,8 |
3 andere Folgen: auch 12,8,5,3,6..., 12,8,5,3,2,2,3,5,8,12,6...
|
| 12,8,5,3,11,91,667,4953 |
Fak(i)+11+pow(i,2)-(pow(i,3)+i*14)/3
|
| 20,70,190,410,760 |
3 einfache Polynomdarstellungen oder
3 ganz andere Algorithmen
|
| 2,7,19,41,76 |
3 völlig andere Algorithmen und ohne die 0 am Ende
|
| 25,70,175,370,685 |
3 Rekursionen nur mit Polynom Grad 2
|
| 15,3,19,0,0,8,30,25,2,60 |
2 komische Polynome auch 5,22,12,19,4,19,0
|
| 4,8,15,16,23,42 |
Rekursion und Polynom
|
| 20,1,18,4,13,6,10,15,2,17,3,19,7,16,8,11,14,9,12,5 |
A003833 Sectors around outside of darts board
siehe auch Darts Geschichte
|
| 0,1,2,6,13,26,51,97,182 |
Polynom und Rekursion
|
| 1,2,5,10,17,26,29 |
Polynom und floor (Abrundungsfunktion)
|
| 13,36,59,22 |
Polynom, MOD und floor (Abrundungsfunktion)
|
| 19,412,745,1078 |
Polynom, Lin+pow, String
|
| 19,412,745,1078,431011 |
Polynom, Lin+pow, String
|
| 4,12,16,44,72 |
explizit Pow, Reku-Pow, Polynom Basis8
|
| 4,12,16,44,72 |
Polynom, Reku-Prod, Diff
|
| 0,1,2,3,6,11,20 |
Tribonacci-Folge rekursiv und explizit und Polynom
|
Oft gesuchte Zahlenfolgen mit einfachsten (aber wechselnden) Grundrechenarten (meist nur theoretisch ohne praktischen Anwendungsfall):
| 1,3,2,5,4,7,8,9,16 |
in den Augen primitiver Intelligenztestersteller einzige Lösung
andere Startwerte: 0,1,2,2,4,4,6,8,8,16,10...; 2,3,4,5,8,7,16,9...; 3,3,6,5,12,7,24...; 1,3,3,6,5,12,7...
|
| 49,50,48,16,64,69,63,9 |
in den Augen primitiver Intelligenztestersteller einzige Lösung
leichte Variation: 49,50,48,16,64,65,63,21
|
| 6,4,9,7,12,10,15,13,18,16 |
in den Augen primitiver Intelligenztestersteller einzige Lösung
leichte Variation: 2,2,3,6,8,24,27,108; 5,8,3,6,9,4,8,11; 5,3,8,6,11,9,14; 1,1,2,4,6,18,21; 4,7,2,4,7,2,4; 4,2,7,5,10,8,13; 0,0,1,2,4,12,15;
|
| 4,5,7,4,8,13,7,14 |
in den Augen primitiver Intelligenztestersteller einzige Lösung
andere Startwerte: 3,4,6,3,7,12,6,13...; 2,3,5,2,6,11,5,12...; 1,2,4,1,5,10,4,11,19...; 0,1,3,0,4,9,3,10,18; 5,6,8,5,9,14,8,15; 5,5,6,2,5,9,2,8; 5,5,6,3,6,10
|
| 5,5,4,7,9,5,7,9,12 |
§14 in den Augen primitiver Intelligenztestersteller einzige Lösung??
|
| 5,5,4,6,3,7,2,8,1,9,0 |
in den Augen primitiver Intelligenztestersteller einzige Lösung
andere Startwerte: 4,4,3,5,2,6,1,7,0,8; 3,3,2,4,1,5,0,6; 2,2,1,3,0,4,-1,5,-2,6,-3;
|
| 1,2,4,7,11,16,22,29,37 |
A000124 explizit, iterativ, rekursiv; A034856-1
andere Startwerte: 2,3,5,8,12,17,23,30,38,47; 0,1,3,6,10,15,21,28,36; 0,2,5,9,14,20,27,35,44,54; 0,3,7,12,18,25,33,42,52
|
| 2,1,3,4,7,11,18,29,47,76 |
A000032 Lucas numbers explizit und rekursiv
andere Startwerte: 0,1,1,2,3,5,8,13 A000045=Fibonacci numbers; 0,2,2,4,6,10,16,26; 0,3,3,6,9,15,24,39; 0,4,4,8,12,20,32,52
|
| 0,1,1,2,3,5,8,13,21 |
3 NICHT-Fibonacci-Folgen: explizit, aber mit floor/ceil
|
| 1,1,2,3,5,8,13,21 |
3 NICHT-Fibonacci-Folgen: Polynom & floor
|
| 0,1,2,4,7,12,20,33 |
A000071 rekursiv oder Fibonacci(x)-1
andere Startwerte: 0,3,4,8,13,22,36; 0,1,3,6,11,19,32,53;
|
| 0,2,1,2,2,3,4,6,9,14,22 |
A001611 rekursiv oder Fibonacci(x)+1
andere Startwerte: 0,3,2,4,5,8,12,19,30,48; 1,3,3,5,7,11,17,27,43; 0,4,3,6,8,13,20,32
|
| 1,3,4,8,14,25,43,73,122 |
rekursiv
andere Startwerte: 0,3,3,7,12,22,38,65; 0,2,2,5,9,17,30,52
|
| 1,4, 8, 13, 19, 26, 34, 43 |
A034856=A000124+1 rekursiv und explizit
|
| 1,0,1,2,3,8,13,30,55,116,225 |
A113954: iterativ, rekursiv und explizit
|
| 1,2,3,4,5,6,8,9,10,13,14,15 |
2 mögliche Lösungen
|
| 0,1,4,9,16,25,36 |
A000290 rekursiv, explizit, Binom(x,y)
|
| 0,1,1,3,6,9,27,31 |
A019461 rekursiv; Startwert 1 (A019463): 1,2,2,4,8,11,33,37; A019460:2,3,3,5,10,13,39; 62:3,4,4,6,12,15,45
|
| 1,1,2,4,6,18,21,84 |
A019464 rekursiv
|
| 0,3,4,4,7,8,16,19,20 |
2 Lösungen: WVZ + Poly
|
| 1,1,2,4,10,23,49,97,182,328 |
Rekursion mit interessantem Mod 2: 3 gerade und 3 ungerade
|
| 5,2,6,2,8,3,15 |
Vergleich Rechenartwechsel mit Polynom
|
| 33,66,22,18,90,15,8 |
Vergleich Rechenartwechsel mit Polynom
|
| 4,-1,-2,5,-8 |
NK von A200385, Polynom oder Iteration
|
| 13,4,16,8,32,26 |
3 unterschiedliche Lösungen
|
| 2,6,9,18,21 |
2 mögliche Lösungen oder A156222 ; (auch 0,3,-9,-6,24,27,-135,-132,792,795)
|
| 2,3,5,10,24,65,187,552,1646,4927,14769 |
2 mögliche Lösungen (auch 2,3,5,10,24,65,171,408,878,1727)
|
| 3,2,4,4,5,6,6,8,7,10 |
3 mögliche Lösungen
|
| 2,6,5,15,13,39,36 |
2 mögliche Lösungen
|
| 2,8,6,24,22 |
3 mögliche Lösungen
|
| 19,7,10,23,27,13 |
2 mögliche Lösungen
|
| 1,3,2,4,3,5 |
4 mögliche Lösungen
|
| 2,4,6,4,6,8,6,8,10,8 |
2 mögliche Lösungen
|
| 3,6,4,8,6,12,10,20 |
2 mögliche Lösungen
|
| 1,6,3,8,5,10,7,12,9 |
2 mögliche Lösungen
|
| 1,2,6,15,31,56,92 |
2 Algorithmen
|
| 3,3,5,15,19,95,101,707 |
2 mögliche Lösungen
|
| 11,34,17,52,26,13,40,20,10,?5,16 |
Collatz oder Polynom
|
| 1,0,-1,0,1 |
3 unterschiedliche Folgen: Euler, Periode, Polynom
|
| 7,11,23,59 |
3 Zahlenfolgen mit 4 Algorithmen
|
| 3,7,11,23,59 |
3 andere exotische Zahlenfolgen
|
| 5,50,10,45,20,35,43,12,95 |
§C1 primitivste rekursive Lösung oder §C2 Prinzahldifferenzen
|
| 5,50,10,45 |
§C3: Diff=(-1)^n*(|n|-5); §C4=§C3+floor(atan); §C5: Polynom mod 137
|
| 5,50,10,45 |
§C6 rekursiv mod 130; §C7 rekursiv mod 455; §C8 GetPiDezi(13253957019)
|
| 5,50,10,45 |
§C9 wie §C1 einseitig -5; §C10 Polynomdifferenz; §C11 reines Polynom
|
| 12,6,12,7,14,10 |
Polynomlösung + 2 rekursive Lösungen: -6*2-5*2 oder -6+6-5+7
|
| 8,16,24,36,54 |
3 unterschiedliche Lösungen: rekursiv + Polynom + Fibonacci
|
| 8,16,24,36,54 |
3 weitere rekursive Lösungen
|
| 1,4,8,96,99,198,9,12,24,112 |
2 mögliche Lösungen
|
| 8,17,33,67,100,143 |
4 mögliche Lösungen: floor-min, Polynom, Case, Nachkomma
|
| 3,12,27,75 |
3 mögliche Lösungen: Polynom, Bruch-Iteration, Nachkomma
|
| 0,0,1,2,3 |
4 mögliche Lösungen: floor, Polynom, wechselnde Grundrechenart, Nachkomma
|
| 3,6,10,20,24, |
3 mögliche Lösungen: Polynom, wechselnde Grundrechenart, Nachkomma
|
| 8,6,9,5,10,4,11, |
3 mögliche Lösungen: wechselnde Grundrechenart, Polynom, Rekursion
|
| 11,22,33,44,55,66, |
4 mögliche Lösungen: Polynom, String, Number(String-Dreher), 100/891
|
| 1,5,15,43, |
4 mögliche Lösungen: explizite Fibonacci, Iteration, Polynom, Nachkommastellen
|
| 18,26,146,58,61, |
3 mögliche Lösungen: Quad Mod, Nachkommastellen, Lin Mod Mod
|
| 0,1,4,5,12,13, |
4 mögliche Lösungen: Polynom, 2 getrennte Iterationen, Iteration, Nachkommastellen
|
| 2,4,3,4,12,12,8,36,48,16,108, |
2 mögliche Lösungen: Polynom, 3 getrennte geometrische Folgen
|
| 2,3,6,9,36,41, |
3 mögliche Lösungen: wechselnde Grundrechenart, Polynom, irrationale Zahl
|
| 4,16,6,36,26,676, |
2 mögliche Lösungen: wechselnde Grundrechenart, Polynom
|
| 1,3,-2,-6,4,12, |
3 mögliche Lösungen: Polynom, wechselnde Grundrechenart, wechselnes Offset
|
| 1,3,-2,-6,4,12, |
2 weitere mögliche Lösungen: primitive Rekursion; Hilfsfolge ohne mod3
|
| 8,25,16,15,32,5, |
3 mögliche Lösungen: primitive Rekursion; explizit mod
|
| 8,25,16,2,12,5, |
3 mögliche Lösungen: Polynom mit/ohne floor
|
| 8,25,16,19,26,5, |
Polynom mit 3 möglichen mod oder max
|
| 8,25,16,2,11,5, |
3 mögliche Nachkommastellen
|
| 0,1,4,7,9,10,13,16,18, |
Lösung: rekursiv, explizit sin und mod-floor
|
| 7,19,37,61,91, |
Lösung1: Polynom; Lösung2: Prime + floor
|
| 2,5,10,17,28, |
3 Lösungen: Prime, Polynom, floor
|
| 3,9,21,49, |
3 Lösungen: Polynom, floor, exp
|
| 3,9,21,49, |
3 weitere Polynom Lösungen
|
| 36,30,6,108,33,18,111, |
2 Lösungen
& über 15 weitere Algorithmen für diese Zahlenfolge
|
Folgen mit variabler Rekursionstiefe:
| 2,3,9,65,1025 |
Lösung1 mit ansteigender Rekursionstiefe und explizite Lösung2 aB[i]=f(i,aB[i-1]) mit f(z,x)=f(z-1,Fx(x)) mit f(0,x)=x und Fx(x)=x*2-1
|
| 3,5,17,129,2049,65537 |
rekursive und explizite Lösung
|
| 0,1,9,89,1473 |
Differenz aus rekursiver und expliziter Lösung
|
| 1,2,7,21,51,106 |
mehrfach und einfach rekursiv
|
| 1,2,26,210066388901 |
mehrfach rekursiv
|
| 0,1,79,17017969,70647498200545590 |
nichtlineare Rekursionstiefe aB[i]=f(i,0,aB[i-1]) mit f(i,z,x)=f(i,z+1,Fx(x)*z+1) mit f(i*i,z,x)=x und Fx(x)=x*2
|
Ab hier reicht einfache Punkt- & Strichrechnung nicht mehr aus! Auch Polynome sind hier nicht gesucht:
| 5,8,12,19,28,45,70,110 |
§A4 A079501(6)
|
| 5,8,12,19,28,41,60,87,127 |
§A5 A198094(4)
|
| 05,08,12,19,28,52,91,92,83,37,90 |
§A6 A000796(11686922468), d.h. je 2 Ziffern von Pi ab Nachkommastelle 11686922468
|
| 05,08,12,19,28,26,01,56,02,09,09 |
§A7 je 2 Ziffern von 49/(94*Zeta(3))+7/94
|
| 1,8,15,22,29 |
statt i*7+1 -> 4 andere Lösungen!
|
| 92,79,29,72,52,35,25 |
Lösung
|
| 92,79,27,52,35,23,12,11 |
Lösung 1 |
| 0,500,866,1000 |
Lösung 1 (und nur zur Info
Polynomlösung 2)
|
| 5,13,23,37,47,61 |
Lösung, die von vielen erwartet wird
|
| 5,13,23,37,47,35 |
andere Lösung für die, die mehr als einen Schritt weit denken
|
| 5,13,23,37,47,79,502 |
andere Lösung für die, die noch gerade Zahlen erwarten und keine Tricks (Knicke, Modulo, if) sondern ´´weiche´´ explizite Formel im Reellen suchen
|
| 4,6,18,13,20,220,207,224 |
Lösung 1
|
| 222,345,468,5811 |
Lösung 1
|
| 11,111,1100,10010,11001 |
Lösung 1 Diese Lösung scheint mir logischer, als die bei www.testedich.de
|
| 11,111,1100,10010,11001,100010,101100 |
round-pow-Lösung Hier ein Beispiel, wie der Iterationsrechner selbst eine aus Tippfehlern (www.testedich.de) entstandene Folge ohne if und Modulo generieren kann.
|
| 1,3,8,17,30,45,64,86,122,151 |
%02k%06%1D$i%7Bu2rtj%02%1A%04%00$%7C%1C%08%13%7B$%7Dd:?%1C2#+:#jt%08%08s'xx6q,%7Bruj%02%1A-g~d%10%7B%06%1Dt%14%04~%10%01e
|
| 124579,245791,457912,579124,791245 |
Lösung 1
|
| 258371,583712,837125,371258 |
Lösung 1 (und nur zur Info
Polynomlösung 2)
|
| 0,1,1,2,4,9,20,48,115,286,719 |
explizite Näherungslösung zu A000081 (ersten 10 Glieder stimmen)
|
| 0,1,1,2,4,9,20,48,115,286,719 |
explizite Näherungslösung zu A000081 (ersten 15 Glieder stimmen)
|
| 1,1,2,3,4,5,7,10,14,19,27 |
%02%08%16bkgsb(fmale%04%0C%0Dc%11%15%7B%13%06d%17s1%0B%1Da%1Fi6-8OE%60%00+mdcgk&%7B%60y%14%0A%02%0EH%7Cu%00+m=cu%10%0D/%0C%7F&+7#E%09%08%05:%18%7Dq/%14%14/%0C%7F%14%06+%10%0Ca%0A/~t%09q%0E%1E&cb%07ep%02%03%10a%06v%13%0Bw
|
| 3,4,5,7,10,14,9 |
3 Lösungen: Poynom, Iteration, pow-floor
|
| 1,3,2,3,9,6,2,6,4,3,9,6,9,27 |
Modulo-Lösung zu A120879 (vergl. 1. Zahlenreihe 3,9,6,9,27 oben!)
|
| 1,2,6,3334,327788,38809212 |
Lösung 1
|
| 1,6 29,118,452,1704,6421,24294,92360 |
%02k%06%1D%05%16z%13m%7F%7D5%7Fa%7F%02%0E%11%7Cuth$%10%11~%0Drwj%02%1A%04%00$%7C%1C%0A/=*9b'z%7Dmbn=opd%0CHbt~wo%0A%0D9dw%0C%7F%7C%06+#NL%60/yw%7F~b9dtxi%14%07+%10%0B%13aia~5%0E%159dw%0C%7F%16-,%22L%09!lan%60f'%7B%7Do%7C#%10%1F+%10%0B%09!kblo%0A%009ju%14pm%04%0C%7Caox%06%1Df
|
| 2,5,15,50,176,638,2354,8789,33099 |
%02k%06%1D%05%16z%13m%7F%7D5%7Fa%7F%02%0E%11%7Cuth$%10%11~%0Drwj%02%1A%04%00$%7C%1C%0A/=*9b'z%7Dmbn=opd%0CHbt~wo%0A%0D9dw%0C%7F%7C%06+#NL%60/yw%7F~b9dtxi%14%07+%10%0B%13aia~5%0E%159dw%0C%7F%16-,%22L%09!lan%60f'%7B%7Do%7C#%10%1F+%10%0B%09!kblo%0A%009ju%14pm%04%0C%7Caox%06%1Df
|
| 1,7,20,50,152,468,1560,5070,18200,57356 |
%02k%06%1D%05%16z%13m%7F%7D5%7Fa%7F%02%0E%11%7Cuth$%10%11~%0Drwj%02%1A%04%00$%7C%1C%0A/=*9b'z%7Dmbn=opd%0CHbt~wo%0A%0D9dw%0C%7F%7C%06+#NL%60/yw%7F~b9dtxi%14%07+%10%0B%13aia~5%0E%159dw%0C%7F%16-,%22L%09!lan%60f'%7B%7Do%7C#%10%1F+%10%0B%09!kblo%0A%009ju%14pm%04%0C%7Caox%06%1Df
|
| 0,1,5,61,1385,50521,2702767 |
extrem schwer: %02%08%17+j%04%03gz%0F%16)h%60k%12%04%0Edbn+o,%60zh%7Fmhk%7Bl:gY%0B%7C~checb(etxhl%04%0C$%1C%11s%06%1D%05%16#%13m=)$,0l%045%09Haoh%05%1A#kc%0Awa%02%1At%02%03%11a%06e
|
| 2,4,6,9,12,13,17,19,21,24,26,30,32,33,39,40,45,48,51,54,57,58,67,66,69 | p |
| 1,4,8,13,17,22,27,33,37,41,50,55,62,67,72,82,86,92,99,104,114,117 | p |
| 1,6,12,18,27,33,42,52,60,68,77,85,95,105,112,124,135,143,154,164,176 | p |
| 0,1,2,2.6012189435657951e+1746 |
0, 1!, 2!!, 3!!!, 4!!!!
|
| 1,2,1.5481398284277604e+45 |
mehrfach rekursiv und ultra extrem stark ansteigend (schon bei i=3 nicht mehr darstellbar)
|
| 0,0,0,0,0,0,0,0,0,1,10,83,768 |
extrem schwer: %02:)&+0b+(?n)h8+%25eY%08e%3Ex);-f%00%06l)hfmm%7F%0A%10g%3E%7Ctfcg%10%01%06%13r%09ysvH%1Cy%7D%13%06d%17s%16.-yr%7D%7F#%09z%11%15%7B%13%06d%17c%10%0Dv%0Cy%14%0A%02%0FH%7Cu%00+m=cu%10%0C/%0C%7F%12%25)eH%08s'%17%1E=%17s%10%0D/%0Co%14%07+%10%1Aa%06/vv%11%7B%7B%10%01v%11%0Cd%04%0Cn
|
| 22744,3260,999,427,220,128,81,54 |
extrem schwer: %02-%3E#m,%60%22?(n)ky%3Ci!NF%60%16%1Ao,%60%7Cy%60tzs%7B%3Cm%7C%13%08%08%08%13%07d%17sat/lso%04%01%7D%7C%1C%0E'8mdcu1%0B%1Da%1Fi%04%01%7D%7C%0C%08%04c%18o%0A%00%10%0D/%0C%7F%12%3Cj$%08%1A%08%05:%18i%0C/;g/xy5%00%19$%7C%1C:)&+0bf%10%0D/%0Cm%14%07+%10%0C%10albudz~%60%7Fvxy%14%0A+h%12dys%13%0Bd%0A%00%60%0F%08r
|
| 1,11,21,1211,111221,312211 |
Iterationsrechner Beispiel 100 Folge A005150
|
| 14,1,15,0,16,1 |
Stelle, wo Folgen A079624 und A166514 mit 6 Stellen übereinstimmen
|
| 1,2,2,4,2,4,2,4,6,2 |
§§1 OEIS-Folgen A001223 und A054763
|
| 1,2,2,4,2,4,2,4,243 |
§§2 Polynom
|
| 1,2,2,4,2,4,2,4,2,4,2,4 |
§§3 OEIS-Folge A106469
|
| 1,2,2,4,2,4,2,4,4,8,4,4 |
§§4 OEIS-Folge A193562
|
| 1,2,2,4,2,4,2,4,0,6,0 |
§§5,... Pi Nachkommastellen ab Index 42825937, 48460697, 118973497, 238973985, 130453167966, 4999867590497 usw.
|
| 1,1,2,3,5,7,11,15,22,3? |
asymptotische weiche explizite Näherungslösung zur OEIS-Folge A000041 (ersten 9 Glieder stimmen)
|
| 0,1,1,3,4,8,14,25,46,84 |
A136425 explizit
anderer Offset: 1,2,2,4,5,9,15,26,47; 0,0,2,3,7,13,24,45,83
|
| 0,0,0,0,0,0,3,11,31,77,177 |
A136425-[aB[i+1]+aB[i]+i]
anderer Offset: -1,2,10,30,76,176
|
| 0,0,0,0,0,0,2,4,10,22,48,101 |
A049866-A136425
anderer Offset einer Folge: 0,2,1,4,6,11,19,34,59
oder 2,1,4,6,13,25,48 oder 2,3,5,10,19,36,69 oder 1,3,5,11,23,49 oder 1,3,9,21,47,100
|
| 10,15,25,35,55,65,85,95 |
2 Lösungswege
|
| 5,19,37,59,81 |
3 unterschiedliche Algorithmen: 5,19,37,59,97 oder 5,19,37,59,85
|
| 1,3,4,8,14,16,24,61,80 |
A103002 IsPrim(10^i-7)
|
| 6,9,15,21,33,39,51,57,69 |
A001748 und Polynom
|
| 1,1,3,5,175,441,4851,14157 |
abs(A038535)
|
| 1,1,2,5,15,52,203,877,4140,21147 |
A000110
|
| 0,1,3,9,33,153,873,5913 |
A007489=sum k! {k=1 to n}=(-1)^(n+1) *(1+n)!* !(-2-n)-1-!(-1) explizit!
|
| 55713,55709,55708,55707 |
InStr() und Polynom
|
| 1/9,1/4,3/7,2/3,1/1 |
Bruch mit konst., variablen Nenner, oder Rekursion
|
| 67,15,15,22,21,21,25,57 |
nichttriviale Rekursion mit Variable
|
| 1,3,1,3,2,6,5,15,14,42,42 |
A126324 auch 1,3,2,15,14,126,132,1287
|
| 1,1,4,27,256,3125,46656 |
A000312 auch 1,0,2,24,252 und 1,1,3,22,233
|
| 1,39,945,18225,306180,4684554,66961566,908764110 |
nicht StirlingS2 und Polynom 7.Grades
sondern einfacher 9^x*Binom aus A095661 (3,13,35,75,140,238,...)
|
| 1,2,28,321,5722,155699,6030450,315138601 |
Pochhammer Formel
|
| 0,2,6,12,20,30,42,56,72 |
explizite und rekursive Formel auch 1,3,7,13,21,31,43,57,73,91 oder 1,2,5,10,17,26,37,50,65,82
|
| 0,2,23,355,6697,151081 |
explizite Formel
|
| 1,2,3,9,30,157,980,7609 |
explizite Formel nicht A073950; auch 1,3,5,17,59,313,1959
|
| 1,3,8,33,164,985,6894 |
explizite Formel A001120 auch 2,5,11,41,179,1033,6999
|
| 2,4,9,32,135,768,5145 |
explizite Formel auch 2,2,3,8,27,128,735 und 2,3,6,20,81,448,2940
|
| 1,2,10,61,482,4558,50418,637642,9075584 |
mögliche Formel auch 1,2,10,60,420,3360 und 1,2,11,65,458,3665
|
| 2,9,125,2401,161051 |
3 unterschiedliche Lösungen auch 1,8,124,2400,161050
|
| 26,5,47,26,68 |
2 unterschiedliche Lösungen
|
| -1,0,1,3,7,9,11,12,13,15,17,19,19,21,23 |
A007775(x/2)
|
| -1,1,7,11,13,17,19,23,29,31,37 |
A007775(x)
|
| 0,3,9,12,15,19,21,26,30,33,39,42 |
A007775(x+1/2)
|
| 0,4,9,11,15,18,21,27,30,34,39,41,45 |
A007775(1/2-x)
|
| 0,6,12,24,48 |
3 unterschiedliche Lösungen
|
| 0,6,12,24,48 |
3 weitere Lösungen
|
| 7,9,13,15,19,21,25 |
3 unterschiedliche Lösungen
|
| 1,5,17,37 |
Lösungen
|
| 0,1,5,17,49 |
Lösungen
|
| 1,5,17,53 |
Lösungen
|
| 1,1,5,17,20 |
Lösungen
|
| 1,1,5,17,23 |
Lösungen
|
| 1,1,5,17,94 |
Lösungen
|
| 21,18,16,15,15,16,18,21,25,30 |
Lösungen
|
| 1,0,0,1,3,6,10,15 |
Lösungen
|
| 4,5,7,9,13,15,19 |
Lösungen
|
| 2,5,9,13,19,23,29,33 |
Lösungen
|
| 2,5,9,13,21,25,33 |
Lösungen
|
| 0,1,5,14,39,144 |
Lösungen vergl. 1,2,6,15,40,145 = A004664
|
| 0,2,7,17,43 |
Lösungen
|
| 1,1,4,12,36,140 |
Lösungen
|
| 0,3,8,15 |
3 unterschiedliche Lösungen die mit 24 oder 48 oder 77 fortgesetzt werden kann!
|
| 9,15,25,39 |
3 unterschiedliche Lösungen mit Hilfsfolge 0,2,4,14,32,82,188
|
| 5,25,38,46,57,138,153,162,180,195,201,206,238 |
Polynom-Lösung 1
oder Nachkommastellen-Lösung 2
|
| 5,25,38,46,57,138,153,162,180,195,201,206,238,277,298,320,324,332 |
Polynom-Differenz-Lösung
das Bild der krummen Kurve
|
| 3,0,2,5,8,9,6 |
3 mögliche Lösungen
; 3025896 ist etwa alle 10 Mio. Pi-Nachkommastellen zu finden, d.h. in den bekannten 12.1 Bio. über 1 Mio. mal!
|
| 1,2,4,7,11,16 |
3 anspruchsvollere Algorithmen als a[n+1]=a[n]+n+1
|
| 7,5,6,4,8 |
3 Lösungen: Iteration, Polynom, Ersatz/Replace
|
| 2,1,3,12,13,12 |
3 anspruchsvolle Lösungen: Polynom-Rekursion, Primzahlen, sin
|
| 15,3,19,0,0,8 |
2 Lösungen: Polynom, Nachkommastellen
|
| 5,0,145,0,1649,-2800,18785,-61440,268705 |
3 Lösungen: Potenzsumme cos, Potenzsumme Mod , Polynom
|
| 1,2,7,25,83,265,832, |
abgewandelte explizite Funktionen von A052541(x) , auch 1,2,5,19,71,245,802 oder 1,2,1,1,23,145,622,2258,7561 oder 1,2,7,65,569,4645,39266 oder 0,0,0,3,15,54,177 oder -1,1,1,2,10,43,158,532,1714
|
| 4,5,8,17, |
3 explizite Lösungen: , noch 2 weitere per Plotter unten
|
| 1,5,16,27,16,1,0, oder 1,4,9,8,1,0,1 oder 1,32,81,64,25,6,1, |
3 gegenläufige Potenzen
|
| 1,0,3,-2,5,-4, |
3 Lösungen: cos, floor-pow, floor-XOR-mod
|
extrem schwere Zahlenfolgen aus hypergeometrischen Funktionen (schon die Frage, ob der Nachfolger gerade oder ungerade ist...):
| 1,2,5,15,51,188,731 |
iterative Lösung1; explizite Lösung2: hyg2F1(1/2,1-x,2,-4); x 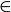 R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen |
| 1,2,4,10,30,102,376,1462 |
iterative Lösung (leichte Hilfsfolge für viele andere schwere Zahlenfolgen) |
| 1,1,3,11,45,197,903,4279 |
iterativ A001003 ; explizit: hyg2F1(1-x,x+2,2,-1); x 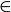 R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen |
| 1,4,48,960,26880 |
explizite Lösung ; x 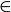 R R |
| 0,8,200,6352,261667 |
explizite Funktion mit Hilfe von (4-AppellF3(-0.25,-1,-x,0.5,0.5,-0.5,-0.25)*...; x 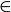 R R |
| 0,24,480,12704,448572,20097321 |
explizite Funktion mit Hilfe von (4-AppellF3(...)*...; x 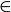 R R |
| 0,0,58,4876,374159,30028746,2600940214 |
explizite Funktion mit Hilfe von AppellF3(...)...; x 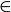 R R |
| 0,11,1678,109508,6226387,346354961 |
explizite Funktion mit Hilfe von AppellF3(...)...; x 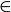 R R |
| 1,-3,756,149676,-5779224,-95809560 |
die doppelt hypergeometrische AppellF4(-0.25,-x...)*8^x*... ;x 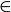 G nur ganzzahlig! G nur ganzzahlig! |
| 0,1,2,3,4,4,5,5,5,5,4,5,5,5,5,4,3,3,3,3,2,2,4,4,4,4,0 |
Lösung bei den Familiengeburtstagskonstanten
|
| 1,2,4,8,13,22,36,53,73,94,109,118,119,120,119,59 |
floor(Gamma2(6,13-x))
|
| 60,33673,101390,142620,145870,4008553,11937122,... |
Nachkommastellengleichverteilungspositionen.htm
|
Dezimalstellen mathematischer Konstanten (constants):
|
Die Funktion GetKoDezi(Konstantenindex,ab Stelle, Anzahl) liefert eine mathematische Konstante als String (>200 Stellen mit Dezimalpunkt). Ein positiver Index stimmt mit research.att überein (dort mit A beginnend). Konstanten, die dort (noch) nicht aufgenommen sind, haben negativen Index.
Konstanten, die sich aus anderen Zahlen kombinieren lassen und in pi.lacim.uqam-Suche zu finden sind, haben keinen Index
(vergl. pi.lacim.uqam-Tabelle und http://pictor.math.uqam.ca/~plouffe/pi/ip/) mehr in http://pi.gerdlamprecht.de
|
| 1.00000000000000000000000000000079976 | -25 exp(x-pi^pi) mit x=exp(-x-x)*(x+1)+PI^PI |
| 1.00001704136304482548818390229983042 | Sum 1/(2k+1)^10 = (1-2^-10)*Zeta(10)= (Pi/2)^10*31/2835 = (A000796/2)^10*31/2835 mit bigc(0add1sub2mul3div4pow5comp6abs7int8round9mod10sqr11exp12ln13Fak14Fib15sin16cos17atan18powr19AGM,str1,str2) |
| 1.00982433184782138082007729601206511 | -4 das lokale Max der expliziten Fibonacci-Funktion x>0 auf 200 Stellen |
| 1.06784882968162500543191460603710205 | ?? A052541(x)=Pi |
| 1.09457610523164567010883054798529946 | -3 ab 10.02.2010 A172197 , bei diesem Argument hat die explizite Fibonacci-Funktion ihr lokales Max x>0 auf 200 Stellen |
| 1.09832777880783619122807570574037383 | -29 gamma(e/Pi) |
| 0.11111111111111111111111111111111111 | siehe A-670 AlmostInteger.htm |
| 0.00000001111111122222222333333334444 | siehe A-60662 und A-60663 in Schnapszahlen |
| 1.12878702990812596126090109025884201 | -43 Gamma(5/6) |
| 1.14472988584940017414342735135305871 | 53510 log(PI) |
| 1.15872847301812151782823350993350914 | 133731 Ziegenfaktor (Goat problem) 323 Mio. Digits; Iterationsrechner Beispiele 3 bis 6 und 36; 10000 Dezimalstellen und Ziffern-Häufigkeit hier |
| 1.19814023473559220743992249228032387 | 53004 AGM(1,sqrt(2)) per 2 + 6 bigc mal 6 Iterationen; vergl. mit Iterationsrechner Beispiel 1 und 61 |
| 1.19967864025773383391636984864114194 | 85984 x=exp(-x-x)*(x+1)+1; x=x-tanh(x)*x+1 |
| 1.20205690315959428539973816151144999 | A002117=Zeta(3)=hyg4F3(1,1,1,1,2,2,2,1); www.gutenberg.org/dirs/etext01/zeta310.txt www.numberworld.org/nagisa_runs/computations |
| 1.22541670246517764512909830336289052 | A68465=Gamma(3/4)=-0.25! |
| 0.12345678910111213141516171819202122 | -51...-54 ab 11.07.2010 A179295 ; irrationale 4 Teile Konstante |
| 1.23596242396942578852259219015134077 | -15 x=exp(-x-x)*(x+1)+pi/3 |
| 1.28694088168916124946323695883865003 | -31 gamma 1/SQRT2 |
| 1.30904091128148126982453252139592957 | -30 gamma(log(2)) |
| 1.31229948555197092909658476270114355 | -16 x=exp(-x-x)*(x+1)+ log(PI) |
| 1.32102058835903519989794071962307366 | -17 x=exp(-x-x)*(x+1)+pi/E |
| 1.35411793942640041694528802815451378 | A073006Gamma(2/3)= = 2*pi/sqrt(3)/A073005 = A019692 * A020760/A073005 http://pi.lacim.uqam.ca/piDATA/gamma23.txt |
| 1.38348099995068943883033885879240867 | [x=exp(-x-x)*(x+1)+1] - [1. neg. Nullstelle Fibonacci(x)] = A085984 - A089260 auf 200 Stellen (als String) |
| 1.41421356237309504880168872420969807 | 2193 sqrt(2) |
| 1.44466786100976613365833910859643022 | 73229 exp(1/e) |
| 1.46163214496836234126265954232572132 | 30169 x bei min Gamma(x) Iterationsrechner Beispiel 25 |
| 1.48635412033351862940750579944547238 | -18 x=exp(-x-x)*(x+1)+e/2 |
| 1.53238603245423827381114726649226240 | -19 x=exp(-x-x)*(x+1)+sqrt(2) |
| 1.54431721079037838813184037292294311 | -xxxx

|
| 1.56746825577405307486334038417968844 | -42 gamma(E) |
| 1.57079632679489661923132169163975144 | 19669 Pi/2 |
| 1.61367900476148355854529993946920795 | 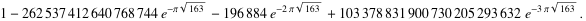 *10^59 nötige Genauigkeit min. 77 Stellen *10^59 nötige Genauigkeit min. 77 Stellen |
| 1.61803398874989484820458683436563811 | A001622=Goldener Schnitt=(1 + sqrt 5 )/2= 2*Cos[(3/5)*ArcSin[Sqrt[3/4]]] = cos(Pi/5)*2=cos(Pi*1/10)/cos(Pi*3/10) |
| 1.64493406684822643647241516664602518 | 13661 Zeta(2) = Pi^2/6 |
| 1.67668837258158419262338474461602607 | -1 oder ab 24.01.2010 meine erste eigene A171909 online: Dezimalstellen des Arguments, bei dem die explizite Fibonacci-Funktion ihr lokales Min hat , Iterationsrechner Beispiel 58 (auch 8 und 60) |
| 1.73081526980064988082780593134971839 | -9 Fibonacci(e) |
| 1.73205080756887729352744634150587236 | 2194 sqrt(3) http://www.numberworld.org/constants.html |
| 1.77245385090551602729816748334114518 | 2161 sqrt(PI)= Fak(-0.5)=gamma(1/2) mit 4020 Nachkommastellen |
| -0.18380235969295560491396901015126673 | 89260 erste Nullstelle von Fibonacci(x)=0 |
| 1.90569572930988389488266643716096670 | -13 ab 14.02.2010 A173201; x=x-(sin(x)-cos(x)*x-PI/2)/(sin(x)*x) oder 2*acos(A133731/2); 10000 Dezimalstellen und Ziffern-Häufigkeit hier |
| 0.19739555984988075837004976519479029 | -44=A105532 atan(0.2) |
| 2.05050407268739758799474811491339475 | -20 x=exp(-x-x)*(x+1)+2 |
| 2.11702705791609991168459841326216067 | -10 Fibonacci(Pi) |
| 2.23606797749978969640917366873127623 | 2163 sqrt(5) |
| 2.28803779534003241795958890906023392 | -41 gamma Pi |
| 2.30258509299404568401799145468436420 | 2392 ln(10) |
| 2.31118116930984015762181895582381468 | Goldener Schnitt + ln(2) = A001622 + A002162 auf 1900 Stellen (als 1 String) |
| 2.33776536666051970277569733788828891 | 4exp(EulerGamma=A1620)/(LambertW(1/e³)+3) |
| 2.38217908799301877455559305252087853 | -(x * LambertW(-(log(x))/x))/(log(x))mit x=Pi; also x^Pi=Pi^x |
| 2.41788522178052771863469034622088301 | -40 gamma 1/E |
| 2.41839915231229046745877101018954097 | 2/3*gamma(1/3)*gamma(2/3)=2/3*(-2/3)!*(-1/3)!=4/9*Pi*sqrt3 Iterationsrechner mit 3 Algorithmen! |
| 2.49290096056092205357608032100227201 | 2*sqrt(2)*ln(1+sqrt(2)) 77 Stellen hypergeometrisch in 30ms oder sqrt(8)*ln(1+sqrt(2)) in 22 s |
| 2.50290787509589282228390287321821578 | 6891 Feiganbaum-Konstante |
| 0.02617694830787315261061168555411266 | sin(PI/120)=(sqr(1+A019812)-sqr(1-A019812))/2 |
| 2.62205755429211981046483958989111941 | 62539 Lemniscate constant (oder Gauss Konstante) = Pi/AGM(1,sqrt(2))=1/2*Pi^(3/2)/GAMMA(3/4)^2*2^(1/2) |
| 262537412640768743.999999999999250072 | 58292 Ramanujan number = exp(Pi*sqrt(163)) |
| 2.67893853470774763365569294097467764 | A073005=Gamma(1/3)=(-2/3)! |
| 2.71828182845904523536028747135266249 | e = exp(1) per bigc(11,x,genau) und GetKoDezi(1113... = A1113; http://www.numberworld.org/ftp/e%20-%20Dec%20-%20500b/ |
| 2.73403703941232006102238175290115647 | -21 x=exp(-x-x)*(x+1)+E |
| 2.81129751467086164212279080371048169 | -39 gamma 1/PI |
| 0.31392594267338226161363271765728631 | -6 Fibonacci(1/Pi) |
| 3.14159264233693430646599057823092228 | 35500000/11300001 |
| 3.14159265301190260407226149477372968 | 103993/33102 |
| 3.14159265358979323846264337879959590 | 1019514486099146/324521540032945 (Johann Lambert) |
| 3.141592653589793238462643383279502884197169399374 | -47 2857198258041217165097342/909474452321624805685313 online: 47 Stellen Stimmen |
| 3.141592653589793238462643383279502884197169399375 | A000796=Pi=hyg2F1(1/2,1/2,3/2,1)*2 Kreiszahl.htm die interessantesten Stellen aus 10 Bio. (engl. numberworld.org) http://pi.gerdlamprecht.de |
| 3.14159265358979323846264338327972661 | log(262537412640768744)/sqrt(163) online: erforderliche Genauigkeit min. 40 Stellen |
| 3.14159265361893662339750030141060161 | 312689/99532 |
| 3.14159292035398230088495575221238938 | 355/113 |
| 3.14412214108074545939751126063983231 | 3+1008449087377541679894282184894/6997183637540819440035239271702 Jacob Marcelis |
| 3.14922373129009411203541721229134753 | -22 x=exp(-x-x)*(x+1)+Pi |
| 0.31830988618379067153776752674502872 | A049541=1/Pi=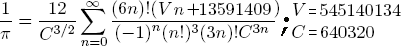 kann mit bigc online berechnet werden: 1/GetKoDezi(796... kann mit bigc online berechnet werden: 1/GetKoDezi(796... |
| 0.32508257437902063419621906537982664 | -5 Fibonacci(x)-Fibonacci(x-1)/2 = 0 um 0.32 (Iterationsrechner Beispiele 8, 58 und 60) |
| 3.28645055277941042287825719377292906 | A172084 x bei AGM(3,x)=Pi suche x in AGM(3,x)=PI (online! mit IM=2;) |
| 3.29549749336057809596679956143506492 | e+Euler = A001113 + A001620 auf 450 Stellen (0.1=Dezimaltrennzeichen) |
| 0.33011421485287020288932958877228268 | -11=A172169 x=Fibonacci(x) siehe Beispiel 59 40 Iterationen und mit Konvergenzbeschleunigung nur noch 4 Iterationen |
| 3.62560990822190831193068515586767200 | 68466=Gamma(1/4)=-0.75!=sqrt(sqrt(PI)^3*sqrt(2)*2/AGM(1,sqrt(2))) |
| 36.4621596072079117709908260226929234 | -23 x=exp(-x-x)*(x+1)+PI^PI |
| 0.38274177378682121467897957182541776 | -7 Fibonacci(1/e) |
| 4.59084371199880305320475827592915200 | -38=A175380 gamma 1/5 |
| 0.46364760900080611621425623146121440 | 73000 atan(0.5) |
| 0.05233595624294383272211862960907841 | A019812 sin(3°)=sin(PI/60)=(sqr30+sqr10-sqr6-sqr2)/16+(1-sqr3)*sqr(5-sqr5)/8=sqr2(sqr3-1)(sqr5-1)(2+sqr3-sqr(5+2sqr5))/16 Iterationsrechner Beispiel 62 |
| 0.54030230586813971740093660744297660 | 49470 cos(1) |
| 5.44417774658383892248063483796386709 | PI+log(10) = A000796 + A002392 auf 1900 Stellen (0.1=Dezimaltrennzeichen; Iter statt Reku, da Reku per Browser begrenzt) |
| 5.56631600178023520425009689520772611 | -37=A175379 gamma(1/6)=gamma(1/3)^2*(3*sqrt(Pi))/(2^(1/3)*sqrt(3)*Pi)
|
| 0.56886448100578310727830792668468187 | -8 Fibonacci(1/2) |
| 0.57721566490153286060651209008240243 | 1620 C=EulerGamma= Euler-Mascheroni-Konstante |
| 0.626657068657750125603941321202761313 | -60 sqrt(Pi/8)=sqrt(pi)*sqrt(2)/4= gamma(1/2)*sin(Pi/4)/2=gamma(3/4)/gamma(1/4)*K(1/sr(2))= FresnelC(∞) |
| 6.548062940247824437714093349428996262 | -36 gamma(1/7) |
| 0.66170718226717623515583113324841358 | 73012 Robbins constant 4/105+17/105*2^(1/2)-2/35*3^(1/2)+1/5*ln(1+2^(1/2))+2/5*ln(2+3^(1/2))-1/15*Pi |
| 0.69314718055994530941723212145817656 | 2162 ln(2) |
| 0.72446216360269026202810513966327235 | -14 x=tanh(x)*x-x+1 |
| 0.72973525686538534226947336908529320 | ??? PhysikalischeKonstantenMathematisch |
| 7.38905609893065022723042746057500781 | 72334 exp(2) |
| 0.73908513321516064165531208767387340 | 3957 x=cos(x) schneller: x=x-(cos(x)-x)/(-sin(x)-1) |
| 7.53394159879761190469922984121513362 | -35 gamma 1/8 |
| 0.76422365358922066299069873125009232 | 64533 Landau-Ramanujan |
| 0.78539816339744830961566084581987572 | Pi/4=A3881 |
| 0.00000000000000000000000000000079976 | -24 x-pi^pi mit x=exp(-x-x)*(x+1)+PI^PI |
| 0.80901699437494742410229341718281905 | A019863=[1+sqrt(5)]/4 = cos(Pi/5) |
| 0.83462684167407318628142973279904680 | 14549 Gauss-Konstante=1/AGM(1,sqrt(2)) Iterationsrechner Beispiel 1 |
| 0.84147098480789650665250232163029899 | A049469=sin(1)=hyg0F1(3/2,-1/4) |
| 0.84721308479397908660649912348219163 | 96427 Gauss-Legendre-Iteration AGM(1,1/sqrt(2))=1/AGM(1,sqrt(2))/sqrt(2)=1/(A14549*A2193)= A53004/A2193 |
| 8.48230016469244174384913713485465778 | -45; Pi*2.7 siehe http://pi.gerdlamprecht.de |
| 8.52268813921947595051439221443955975 | -34 gamma(1/9) |
| 0.88560319441088870027881590058258873 | 30171 min Gamma Iterationsrechner Beispiel 25 |
| 0.88658142871925912508091761239199431 | -32 gamma(SQRT(2)) |
| 0.89567315170528786088696121670097860 | -27 gamma(golden ratio) |
| 0.89694638742460617291260037106876544 | -2=A172081 , das lokale Min der expliziten Fibonacci-Funktion bei x>0 auf 200 Stellen |
| 0.90640247705547707798267128896691800 | A068467 = Gamma(5/4) = 0.25! = (0.25-1)! * 0.25 = A68466/4
|
| 0.91596559417721901505460351493238411 | 6752 Catalan's constant 1 - 1/9 + 1/25 -... |
| 0.93116988340192535799881187389478478 | -28 gamma(Pi/e) |
| 0.93247222940435580457311589182156338 | cos(Pi*2/17)={sqr17-1+sqr(34-2sqr17)+sqr(68+12sqr17+2(sqr17-1)sqr(34-2sqr17)-16sqr(34+2sqr17))}/16 |
| 0.93754825431584375370257409456786497 | 73002 Zeta(1,2) |
| 0.94444221354881717123456789128998936 | -46 sin(Pi*11/92)/sin(Pi*8/63) siehe http://pi.gerdlamprecht.de |
| 0.94444337820557904649220860421297849 | -12=A173571 ; a im Iterationsrechner Beispiel 3 oder sqrt(1-(1-A133731²/2)²)=sqrt(1-A072112^2) |
| 9.51350769866873183629248717726540219 | -33 gamma 1/10
|
| 0.99999999999999999999999999999997806 | -26 pi^pi/x mit x=exp(-x-x)*(x+1)+PI^PI |
| 0.99999999999999999999999999999999999 | A181693 ; siehe A-641 ff AlmostInteger.htm |
| Fortsetzung siehe: | mehr in http://pi.gerdlamprecht.de und Liste-mathematische-Rekorde |
Pseudo-Zufallsgeneratoren (oder vermischte Algorithmen), die garantiert in keiner Knobelaufgabe auftauchen werden:
| 1,41,83,87,155,194 |
%02k%06%1D$i%7C%7D%60%7Cparery%0Dc%11%15%7B%13%07e%17s%10%0Dt%0C%7F%14%06q%10%1Ca%0Ar%0Ex%14%08%7B%0Drwcq%60ppu%16%11%7C%7D2%01%0Fz%13m~tbv%60vzz%11%15s%25nwe~ydwugvc%7F%02%03ab!%1Bn$%10%11~%0Dt'%15%19d%19%7Fe@e%13v%0Eo5ckbz%25j%02%16-%1Fp@e%13v%0E%60f%7F%7Cg~ccrypqvao!c%60%00l%0A%00%60%0F%08a%02%1Ag
|
| 141,283,424,566,707,849,991 |
%02k%06%1D$i%7Bu%10%01%06%12+%09y%12%04%0B%09!mblo%0A%0C9%12%7B7.;+0e%09a%0B/%0Eh2&!?=n%11%01=%19kd%0B%10xvclo%0A%009ju%14sg%04%0C%7Caox%06%1Df
|
| 5,5,4,7,9,5,9,9,7 |
§5 konstruierte Lösung , die absichtlich nicht die Lösung der Aufgabe 14 von
www.testedich.de ist! §6 Weitere Pi-Nachkommastellen-Lösung (5,5,4,7,9,5,7,7,8,1) !!!!
|
| 1,23,456,7805,2913,588595,7638876 |
Pi-Nachkommastellen-Lösung (>186 Mio...)
|
| 804952,1622666070,595827881,1489519853 |
Zufallsgenerator2
|
| 5,5,4,7,9,5,7,9,5 |
§21 Polynom als Index von Primzahldifferenzen
|
36,34,26,7,15,23,17,10,17,5,12,14,5,16,34,?5,22,?5,??,21,2?,2? |
%12yrf?!,/%3C#ebt%7F%3Ch~%19%12pibuag%0E%007jck~rqz%0E%12~vx%05%042bcflcuekpy%11%0C%08%16+i%60cdd%7Cibt%7F%04%125%0D%14alb%7C%7B%7C~%7D%0F%16)nbmh%7C%12%0E%7Bpcn%14%1A6%7Cxo~wbt%02%03@bu%07!753fcyjbvxvta%16%0Dys%7Fwgf%7Fgcwanesnx%0D%10zjbqx%7Fbayjbvxwwa%13%13dwfief%7Cact%60nfrkvao%08%04:%18i8!%25!%22y%04,l+d%0A%09qwguczc9eu%60sgwv%7C%12%0E~vx,~#db~%7F%60wfw%7Bb%10%19xk%13%15=f%7Dyeqcw%60%7Dsb%15%19c%06%03,x~gz~saulum%7C%15%15e%06%03,x%7Fgz%7Cvfs%7B%7Crfaq!jel~~%7Fi%60qcr%7Dn$!NN:n:jlcgu%7Dsbuo%04%0C$%04%12%0Dta%05%1Az%0E%1E%7F%06%1Fa
|
36,34,26,7,15,23,17,10,17,5,12,14,5,16,34,35,22,15,1,21,21,26,5,22,33,25,11,1 |
%10xvd%7Dms=!=2yp%7D73?U%09zo%7Crd~%7Fd~kbpmtzy%0BR94'mfcag%7Fr%60veip%7F%14%19xtfo';%3C$gtx1%2566e%12%08gqcqe~%7F%7D~uawdqr%3EPS%3Cn%60l%7B%7D~d~r%60iert~%14%12z5%227%20b%7Cy%3C7#6%7Cskb%16%11%7Cwgt%7F~xh%7Cuat'509%09%16aidu%60%7Bzadpbw%60rr%3EPS%3Cnal$#ag%7Fr%60veoq~%11%19yra5=ey%60%7Bwes
|
| 3,-56,36,34,26,7,15,23,17,10,17,15,41,40,31,34,14,13,24,13,43,25,34,22,20,20,39,34,17,26,10,26,45,5,28,18 |
Rekursion mit 8 Vorgängern
|
| 32,606,8555,99849,1369564,14118312,166100506,1816743912,22445207406,241641121048 |
bis zu welcher Nachkommastelle findet man alle String/Zifferkombinationen
|
36,34,26,07,15,23,17,10,17,05,12,14,05,16,34,35,22,15,01,21,21,26,05,22,33,25,11,01,30,28,06,20,06,28,15,17,33,34,35,12,12,16,49,...
meine Antwort auf "Zahlenreihe in einem alten Matheheft aus China" (habe noch zig Stellen mehr!)
3D-Zufallsgenerator ohne Periode (könnte irrationale Zahl sein?)
9,1,9,0,2,2,3,9,4,2,2,0,1,3,5,9,3,9,8,3,4,3,3,6,4,9,8,1,2,0,8,6,1,9,3,0,6,8,2,1,8,3,9,3,2,1,4,3,5,0,9,9,9,8,4,2,8,1,0,1,...
eine von über 13460 Folgen mehr Iter3...
8,3,2,6,5,8,2,7,8,4,3,0,5,1,2,1,3,0,1,0,5,8,6,2,0,8,2,4,6,9,7,1,2,1,8,4,7,3,7,2,2,1,2,3,6,2,2,2,5,5,0,3,7,9,6,3,1,6,2,4,...
oder
2,4,5,2,2,3,0,2,7,2,6,3,2,3,1,0,3,5,2,9,2,3,6,4,2,2,8,8,8,2,3,7,1,0,3,0,2,5,3,3,4,0,3,0,3,2,8,4,6,5,5,0,5,7,7,0,9,9,2,2,...
oder
6,2,7,0,8,8,6,4,5,6,4,4,3,1,0,4,7,1,6,3,3,1,6,2,4,3,6,7,8,8,9,2,0,4,3,2,4,9,1,5,7,4,3,0,4,8,4,0,0,5,1,0,1,9,9,8,4,3,5,4,...
oder
7,4,2,9,7,6,4,0,4,9,9,7,0,8,5,8,0,0,0,9,6,7,9,4,9,9,3,8,4,8,1,1,8,0,5,3,7,3,8,5,7,2,5,3,4,1,2,5,8,8,7,6,3,2,6,9,5,3,6,5,...
eine von über 13330 Folgen mehr Iter5...
Exotische Zahlenfolgen mit pseudomathematischen Funktionen wie Quersumme und Kindergarten-Ausmal-Funktion
LINKS:
Mathematische Konstanten online per hypergeometrischer Funktion
132 Algorithmen für die Zahlenfolge 0,0,0,1,0,0,1,1,0,1,1,1
5 Algorithmen für die Zahlenfolge 10,15,9,31,74,77,103,255,390
http://oeis.org/?language=german
http://oldweb.cecm.sfu.ca/projects/ISC/ISCmain.html
http://www.numberworld.org/
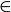 R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen
R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen 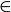 R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen
R reell!! siehe wissenschaftlicher Online Rechner mit vielen hypergeometrischen Funktionen  R
R R
R  R
R  R
R 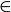 R
R 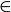 G nur ganzzahlig!
G nur ganzzahlig!  *10^59 nötige Genauigkeit min. 77 Stellen
*10^59 nötige Genauigkeit min. 77 Stellen kann mit bigc online berechnet werden: 1/GetKoDezi(796...
kann mit bigc online berechnet werden: 1/GetKoDezi(796...