Fast ganzzahlig, Muster in Nachkommastellen – Almost Integer, Patterns in decimals |
(Here is the answer to the question: why do you need so many digits...)
Inspiriert von der Seite http://mathworld.wolfram.com/AlmostInteger.html hier noch weitere Zahlen, die extrem dicht neben einer ganzen Zahl liegen.
Hinweis: Rundungsfehler, Brüche wie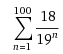 
=0.9...(127*9)...986675837989082575477787...
und einfache Konstrukte wie 1-a^-x sind hier nicht gesucht: nur transzendente
Zahlen mit unendlich vielen Nachkommastellen (ohne Periode).
1. A-641
Mit Hilfe der cos-Funktion wird aus der Umstellung der Ramanujan Konstante A060295 nach Pi:
cos(log(640320^3+744)/sqrt163)
= -0.99999999999999999999999999999999999999999999999999999999999997497129124211…
61 * 9
2. A-642
Mit Hilfe der guten Pi-Näherung A-640 (x ist A111310 umgestellt nach Pi/4) und der gegen Pi/4 konvertierenden Iteration im Iterationsrechner Beispiel 78 b=Iter... erhält man:
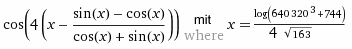= -0.99999999...999972779703543123879375702298…
187 * 9
3. A-643
Mit jeder vorn angestellten Erweiterung um cos(Pi*… verdoppelt sich die Anzahl der Neunen:
=
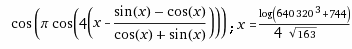-0.99999…999999963435852574731776877915285825…374 * 9
usw.
Alle Konstanten sind mit mehreren 1000 Stellen in http://pi.gerdlamprecht.de.
4. Iteration nahe
einer ganzen Zahl
Die Iteration x=exp(-a*x)/(x+1)+a^a konvergiert sehr nahe a^a. Die Funktion f(a)=a^a/x liegt dann nur minimal unter 1.0:
f(4)=A-644=0.9999999999999999999999999…999999999999999708742282048276387724405065745496345418900…
449 * 9
f(5)=A-4392=0.9999999999999999999999999…99999999999999985582788608255142959612298383684072585509…
6792 * 9
5. Der Arithmetisch-geometrisches
Mittelwert ist geradezu prädestiniert um transzendente Zahlen mit Mustern
zu erzeugen:
agm(1-x,1+x) mit x=10^-38 ergibt schon mal 76 * 9 :
A-645=0.999999999999999999999999999999999999999999999999999999999999999999999999999974
99999999999999999999999999999999999999999999999999999999999999999999999999921874
999999999999999999999999999999999999999999999999999999999999999999999995703124
9999999999999999999999999999999999999999999999999999999999999999999997137451171874
999999999999999999999999999999999999999999999999999999999999999789581298828124
99999999999999999999999999999999999999999999999999999999999998357486724853515624
999999999999999999999999999999999999999999999999999999999866483211517333984374
999999999999999999999999999999999999999999999999999999988825182430446147918701171874
999999999999999999999999999999999999999999999999043884989805519580841064453124
99999999999999999999999999999999999999999999991677527563297189772129058837890624
999999999999999999999999999999999999999999265498568638577125966548919677734374
9999999999999999999999999999999999999999344378734218707904801703989505767822265624
999999999999999999999999999999999940922559085123566546826623380184173583984374
99999999999999999999999999999999463373705226398868717296863906085491180419921874
999999999999999999999999999950919369735473640758982583065517246723175048828124
99999999999999999999999999548414151619326706126045234412913487176410853862762451171874
999999999999999958232330875292353665646782889808719119173474609851837158203124
99999999999999611899649291975634776024652039527751412606448866426944732666015624
999999999963789887864195000108909010781699233660901882103644311428070068359374
9999999966091333235073087911933963591233111289913182417876669205725193023681640624
996814134492703561799560244601541513474740607847479623160324
99074935913085937469977729857292466032678635649362625342599641964369538982282392680644
989013669038119739662939010169342749797805126638246264736409329998423345386981964111059394…
ab hier wird es
bunter: x=1/(10^27+1) mit 54 * 9 + Muster
0.999999999999999999999999999999999999999999999999999999
7500000000000000000000000004999999999999999999999999991
7187500000000000000000000131249999999999999999999999792
5781250000000000000000003320312499999999999999999994584
6557617187500000000000090102539062499999999999999847218
7805175781250000000002634860229492187499999999995388767
3377990722656250000081716449737548828124999999853644681
6921234130859375002644951090812683105468749995183149844
2124575376510620205490779717266559600830077962191424142
6857188344001773036372125053312629461288446533497762626
9828760996461019527799704872886650264262956349720822814
5245811901990299435488029280531918629996948531060760032…
und es geht immer
weiter: x=1/(10^66+1): mit 133 * 9 + Muster
0.999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
7500000000000000000000000000000000000000000000000000000000000000004999999999999999999999999999999999999999999999999999999999999999991
7187500000000000000000000000000000000000000000000000000000000000131249999999999999999999999999999999999999999999999999999999999999792
5781250000000000000000000000000000000000000000000000000000000003320312499999999999999999999999999999999999999999999999999999999994584
6557617187500000000000000000000000000000000000000000000000000090102539062499999999999999999999999999999999999999999999999999999847218
7805175781250000000000000000000000000000000000000000000000002634860229492187499999999999999999999999999999999999999999999999995388767
3377990722656250000000000000000000000000000000000000000000081716449737548828124999999999999999999999999999999999999999999999853644681
6921234130859375000000000000000000000000000000000000000002644951090812683105468749999999999999999999999999999999999999999995183149844
2124575376510620117187500000000000000000000000000000000088303279717266559600830078124999999999999999999999999999999999999837191424142
6857188344001770019531250000000000000000000000000000003016840875053312629461288452148437499999999999999999999999999999994385060262626
9828760996460914611816406250000000000000000000000000104915983298622886650264263153076171874999999999999999999999999999803273548947814
5245811901986598968505859375000000000000000000000003700466982169905531918630003929138183593749999999999999999999999993019392877166282
4658505996922031044960021972656250000000000000000132026436698466527104756096377968788146972656249999999999999999999749699029080707265
3791465199901722371578216552734375000000000000004755686027582888590643506177002564072608947753906249999999999999990946049733593490892
8845032960452954284846782684326171875000000000172691596497339679934768241764686536043882369995117187499999999999670045800244714568048
9315466843436297494918107986450195312500000006314411934682536734551039359075730317272245883941650390624999999987897871035311102921008
4980105993635035588340542744845151901245117419772473479401412678761254526627055838616797700524330139160156249553622429348650337524851
7926131633370978590846789302304387092590340620213176932676536582718319814272467382920694944914430379867553694391953832219497364375220
0407431663178869918340296862879768013954481673892619947967617121276114717197402992354682282893918454647063…
A-647=
... und noch kurioser und bunter sind die Konstanten A-662 und A-663 (mit Abwandlungs-Faktor; curious pattern in transcendental decimal):
und hier schon fast fraktale Strukturen: ein Grund, wozu man 10000 Nachkommastellen braucht
(and here almost fractal structures: one reason why you need 10000 decimal places)
agm(...)/9 mit x=1/(10^126+0.5)=A-670=
Eine noch dichtere Konvergenz nahe 1 zeigt die Form agm(1-x,1+x)/agm(atan(x)/x,sin(x)/x): statt eine Verdopplung gibt es eine Verdreifachung. Bei x=10^-27 ist
A-4403=0.9999999999999...9999999999819444444444444...4444444444424305555555...55555489034047067901234567901...
108 * 9 und 52 * 4 und 49 * 5
analog mit der 38:
siehe auch 4 Bereiche Konstante (4partconst.htm)
6. Offensichtliche Funktionen wie tanh(x)=1-2/(exp(2x)+1), 1 /Zeta(x) und erf(x) in den Konstanten A-652 bis A-657 und A-4376 bis A-4383
A-460288 = f(1) = 0.9817667062541823935289869085468773862984...
A-460486 =f(199)= 0.9999999... 345*9 ...9799740833150310094740165304644853957446...
Aufgabe: Gesucht ist eine Formel, die mit der Zahl Pi auf mindestens 250 Dezimalstellen übereinstimmt. (We seek a formula: over 250 decimal digits are identical with pi.)
Randbedingung: nur die 4 Grundrechenarten +, -, *, / und die 2 Funktionen sqrt(x), exp(x); nur ganzzahlige Faktoren (integer factors) < 1000000.
Lösung (solution): a1*tanh(a3)*tanh(a5)/tanh(a2)/tanh(a4)=
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648569753...
258 Dezimalstellen stimmen mit Pi überein! (258 decimal places are consistent with Pi)
a1=1c696b/bc0bf+(66f6*sqrt(a))/1dc19+(afa1fc*sqrt(c/a))/d00d6+(6cadc*sqrt(b))/d00d6+(dcc*sqrt(d/a))/bc0bf-(bffc4c*sqrt(c))/d00d6-(f9d9*sqrt(6))/1dc19+(994cc*sqrt(d))/d00d6
a2=6bbab6/4fa1b+(d4ab6*sqrt(a/b))/cbcd+(994fd6*sqrt(a))/4fa1b+abd4d0/(cbcd*sqrt(b))-(d6914*sqrt(c))/cbcd-(4ca1ba*sqrt(d))/4fa1b+(caf1aa*sqrt(10))/4fa1b+(ac910*sqrt(14))/4fa1b
a3=9dbcb/(add4*sqrt(a))+(af4fd9*sqrt(c/a))/16644+(496a9*sqrt(b))/add4+(16994d*sqrt(d/a))/cc4f+(90d9*sqrt(c))/cc4f+(9061b*sqrt(d))/11096-fddcd/fbaa-(b4abbd*sqrt(b/a))/11096
a4=(6cd*sqrt(b/a))/aa4+(b1949*sqrt(a))/c9c+(101d09*sqrt(b))/bf0f-c440d1/(1904*sqrt(c))+1b6f19/(b40*sqrt(d))+90a4d/(1904*sqrt(10))+69fd9/(c44*sqrt(14))-f169c/bf0f
a5=1111c1/10a4-(a00091*sqrt(b/a))/c1a+bc1acc/(ac6*sqrt(a))+(4ab16c*sqrt(c/a))/10a4+(9d9d*sqrt(b))/64+(ddd*sqrt(d/a))/ac6-(1046d*sqrt(c))/ba-(cb6fb*sqrt(d))/ac6; a,b,c,d,f Ziffern
7. Konstruktionen mit Wurzel in den Konstanten A-1055 bis A-1056
A-1056=
8. Zufällige Nähe
0.9999999999999999999999999999990478469395294073689761924335114218889335013889328480...
kann man auch umstellen: A-1094 = 163/(log(640320^3+744)/pi)^2 =
0.99999999999999999999999999999985756577949415128179154298750627920778001...
Analog kann man mit A-1092=x=2-ln(x) und geeigneten Brüchen (Nenner + Zähler <10^24) folgende Konstanten finden:
A-1093=
0.99999999999999999999999999999957410515486491259590466629741485821710428...
A-4339=
0.99999999999999999999999999999966840985813106468673984235886653849100799607100...
A-4340=
0.9999999999999999999999999999998342049290655323433699211794332555015012249529200392879...
A-4341=
0.99999999999999999999999999999983420492906553234336992117943324175749845187033905895315...
Diese liegen so nahe beienander, dass man mit A-4341/A-4340 eine noch bessere Annäherung an 1 findet: A-4342= 0.999999999999999999999999999999999999999999999999999999999999986255997226917419019665217...
Die Iterationskonstante A-4397 liegt sehr nahe an dem Pi-Bruch A-4398=(2812494188/15032916293)Pi:
A-4398/A-4397= 0.9999999999999999999999927534802022211679364118715846645584081707209927284422...
Bei A-12042=0.123456789101112...32333434307347066467428...
stimmen 61 Stellen mit A033307 (Decimal expansion of Champernowne constant) überein, d.h. A-12043=[A-12042]/A033307=
0.99999999999999999999999999999999999999999999999999999999999914432301757920921129...
Der Bruch 1209493/4900500 und A036211 (als Zahl statt Folge der geraden Zahlen, also 0.246810...) stimmen mit 94 Dezimalstellen überein. Per agm und Wichtungsfaktoren A-16253 bis A-16256 konnte ich die Genauigkeit auf 174 Stellen verbessern:
A-16257=02468101214161820222426...98100102104106108110112114116118120122124126128130132134136138140142144146148150143...
Der Quotient beider liegt demnach nahe 1 (173*9): A-16257/A036211 =
0.9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999963266003...
Der Bruch 6343856911176540959417/2019312371362858600511 und Pi stimmen etwa mit 42 Stellen überein. Per agm(1-x,1+x), x=154643*515653*17523976206217645441*1730362710642184807323418351*3/2^57/5^57/10^22 stimmen etwa 101 Stellen. Die 2malige Anwendung der Selbstkonvergenz gegen Pi/4 (siehe im Iterationsrechner Beispiel 78 b=Iter... ) ergeben dann 916 übereinstimmende Dezimalstellen von Pi:
[A-57818]/Pi = 0.999999...(916*9)...99990737125702271781533178217369344647726085496958642173653888713851013575392825101785851763812481973127391600...
29.01.2011 Die in http://www.plouffe.fr/ beschriebene Konstante A-301505 =
119.000000000000000000000000000000095937458510255473355885849133973841504339...
konvergiert nur sehr langsam (5146 exp-Summen für etwa 1060 Stellen). Schon die 1. Näherung auf 73 Dezimalstellen lässt sich sehr viel schneller berechnen:
A-301504 =119/agm(1-[A-301503],1+[A-301503])=
119.000000000000000000000000000000095937458510255473355885849133973841504344...
Der Quotient liegt bei A-301506=A-301505/A-301504=
0.9999999999999999999999999999999999999999999999999999999999999999999999999590312790180718434647922776...
2*sin(pi/42)=((-1)^(10/21)-(-1)^(11/21))
=0.14946018717284850858187949146953330674709751033463388789195276785052582065250892150190993367014516608656409430478669061487486492858280406...
861153051393/970013604091-(1664441666351sqrt(2/3))/415720116039+(1070136902287sqrt(5/3))/970013604091-(2745476249608sqrt(10))/8730122436819-(30541612007sqrt(1/3(3+sqrt(3))))/2910040812273+(582444475981(3+sqrt(3)))/1247160348117-(1317359304046sqrt(2(3+sqrt(3))))/8730122436819+(476734114765sqrt(5(3+sqrt(3))))/1247160348117-(3444459267511(sqrt(2)+sqrt(3)+sqrt(5)+sqrt(3+sqrt(3))))/17460244873638
=0.14946018717284850858187949146953330674709751033463388789195276785052582065250892150190993367014516608656409430478669061487486492858216814...
132 richtige Nachkommastellen!
Alle ohne den unter 3. beschriebenen Konvergenz-Trick mit cos(Pi*...
9. Unglaubliche Übereinstimmung von 26 Nachkommastellen in 2 verschiedenen Konstanten
Bei der Suche von Iterationsformeln mit Konvergenz gegen 1 fand ich zufällig 2 Bereiche, die mit 26 Stellen übereinstimmten:
A-1095 = 1.0000... i= 82 NK=3662551440329218106995884769122085048010...
A-1370 = 0.1111... i=188 NK=3662551440329218106995884773662523586475...
Diese Ziffernfolge 36625514403292181069958847 gibt es zwar auch in Brüchen wie
89/243 = 0.366255144032921810699588477366255144032921810699588477366...
4277/3888=1.10005144032921810699588477366255144032921810699588477366255144032921810699588477...
, aber diese 2 sind transzendent wie Pi:
- ohne Periode
- ohne nachträgliche künstliche Verschiebungen wie x1 + x2/10^x3
- nicht im vorderen Musterbereich (erste 80 Stellen) wie unter 5. bis 7., denn hier vorn kann "konstruiert" werden:
A-4373=
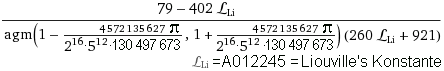=0.03662551440329218106995884770000040311610350465148104574...Hinweis:
Die Wahrscheinlichkeit, in den bekannten 5 Billionen Stellen von Pi eine 15 Stellige Ziffernfolge zu finden, liegt um 0,5%.
"352399548071634" kommt laut Shigeru Kondo und Alex Yee nicht in den 5e12 Stellen vor!
Anders herum geht es leichter: man nimmt sich bekannte Stellen von Pi (z.B. die letzten 37 von 5 Billionen), sucht eine kurze Konstruktion mit viel Übereinstimmung (20 Nachkommastellen) und addiert den fehlenden Rest dazu:
A-4389 =log((310*sqrt(2)+1051*e+65*e^2-304*pi+237*pi^2-240)/3)+((123*2^10-53)*15945966+19)*16939
=34006417497120374.402382642194842838520075360999132024926964667045218949460...
A-12026=3.4006417497120374402382642194842838523750296347061861265191674510876019184719...
10. Inseln in den Nachkommastellen
A-4401=
=
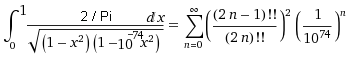Leicht abgewandelt bekommt man eine wunderschöne Konstante, die ab der 699 Nachkommastelle eine Insel aufzeigt: 60 mal die Ziffer 6:
A-4400=0.00584795321637426900...3519694010416666666666666666666666666666666666666666666666666666666666661563307100708721673976608...
A-4400 dezimal 10000 Stellen (60 mal Ziffer 6 blau; vergl. Pi Nachkommastellen in Bilder visualisiert ):
11. Unendliche Produkte
Bei dieser Konstante nimmt die Anzahl gleicher zusammenhängender Ziffern (Inseln) nicht ab, sondern zu (einige Ziffern scheinen völlig zu fehlen -> ob sie bei i>21000 kommen?):
A-12185=
Alle Konstanten sind mit mehreren 1000 Stellen in http://pi.gerdlamprecht.de.
Extrem dicht lassen sich Konstanten nahe e erzeugen, da e = lim (1+1/n)^n, n->∞ (infinity)
So stimmen 18457734525360901453873569 Stellen von (1+9^(–4^(7*6)))^3^2^85 mit mit e überein, da
n=9^(2^84)=3^(2^85)=9^19342813113834066795298816=3^38685626227668133590597632=6.735682469523...*10^18457734525360901453873569
Nachteil: sehr Rundungsfehleranfällig und kein Rechner kann mit mehr Stellen rechnen als Atome im Weltall...
siehe auch Transzendente Schnapszahlen, Familiengeburtstagskonstanten und Mathematische Konstanten nahe Physikalischer Konstanten (Mathematical constants near Physical Constants), Zahl 23 12233344445.html