akustischer Mittelwert bei k=10
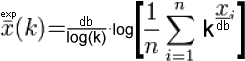 =
Sonderfall:
=
Sonderfall:db-Faktor= (beim Sonderfall k=e=2.71828182845904523536 db=1 werden also die Exponentialwerte gemittelt, die per natürlichem Logarithmus "zurücknormiert" werden)
logarithmischer Mittelwert
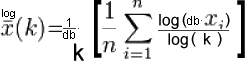 =
=
Gerd Lamprechts Analyse von Folgen |
Wertefolge y[i]: Anzahl n=
Diff= y[i]-y[i-1]:
Quot= y[i]/y[i-1]:
y[i] Mod:
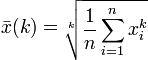 per Schieberegler stufenlos Zwischenwerte berechnen lassen.
per Schieberegler stufenlos Zwischenwerte berechnen lassen.
lineare Verschiebung:
Hölder-Exponent k=
Mittelwert =
Sonderfall:
akustischer Mittelwert bei k=10
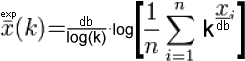 =
Sonderfall:
=
Sonderfall:
db-Faktor= (beim Sonderfall k=e=2.71828182845904523536 db=1 werden also die Exponentialwerte gemittelt, die per natürlichem Logarithmus "zurücknormiert" werden)
logarithmischer Mittelwert
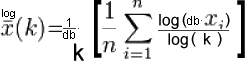 =
=
| harmonisch-geometrisch | arithmetisch-harmonisch | arithmetisch-geometrisch AGM | arithmetisch-quadratisch | arithmetisch-exponentiell | quadratisch-exponentiell |
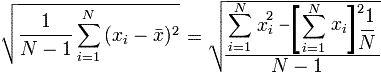 =
= | Variationskoeffizient VarK =σk / AMW= | Schiefe (Wiki engl.: Skewness/s'^(3/2)): | erwartungstreue Schiefe (EXCEL G...n/(n-1)/(n-2)): |
| g= | v'= |
X-Stützstellen zur Wertefolge (editierbar; monoton steigend) x[i]:
Newtonsche Interpolationspolynom-Faktoren p[i-1]:
Polynom-Funktion f(x)=
Polynom-Funktion f(x)=
Polynom-Testrechnung x=
f(x)=
Beispiel (FAQ, Hilfe)
Universal Diagramm (Plotter), Nullstellen Rechner,
Zahlenfolgen
LINKS:
- kubische Splines: http://www.arndt-bruenner.de/mathe/scripts/kubspline.htm#rechner
- http://en.wikipedia.org/wiki/B-spline
- http://de.wikipedia.org/wiki/Ausgleichungsrechnung
- http://de.wikipedia.org/wiki/B%C3%A9zierkurve
zurück zum Iterationsrechner