Beispiele
der von Menschen begangenen Fehler und Irrtümer (Denkfehler)
Schwerpunkt liegt bei mathematischen Fehlern.
aus http://de.wikipedia.org/wiki/Pythagoras_von_Samos
A: Ein Schüler des Pythagoras, Hippasos von Metapont(5. Jahrhundert v. Chr.), soll als erster die Konstruktion des einer Kugel einbeschriebenen Dodekaeders gefunden und auch erkannt haben, dass gewisse geometrische Größen (wie das Verhältnis von Diagonale und Seite eines Quadrats) nicht durch ganzzahlige Zahlverhältnisse ausdrückbar sind (Inkommensurabilität). Eine späte Überlieferung behauptet, Hippasos habe diese Entdeckungen veröffentlicht und damit aus der Sicht der Pythagoreer Geheimnisverrat begangen. Daraufhin sei er aus der Gemeinschaft ausgeschlossen worden und bei einem Schiffbruch umgekommen, was als göttliche Strafe zu deuten sei. Die ältere Forschung interpretierte dies als „Grundlagenkrise“ des Pythagoreismus: Hippasos habe die Grundlage der pythagoreischen Mathematik zerstört, die besagte, alle Phänomene seien als Erscheinungsformen ganzzahliger Zahlverhältnisse erklärbar.
B: "Der Satz des Pythagoras" stammt nicht von Pythagoras von Samos. Schon weit über tausend Jahre vorher war dieser Zusammenhang den Babyloniern bekannt!
§1 Alte Theorien sind nicht immer richtig
a) „Erde ist eine Scheibe und steht im Mittelpunkt der Welt.“
-> Erst 1992 wurde Galileo
Galilei von der römisch-katholischen Kirche formal rehabilitiert.
b) Newtons Bewegungsgesetze stimmen bei hohen Geschwindigkeiten oder großen Gravitationskräften nicht (Relativirätstheorie)
§2 Was im Internet oder Büchern steht, ist nicht immer richtig:
A) Das Primzahlpolynom
ist mindestens 3-mal falsch dargestellt (Link enthält Quellenangabe)
B) xyz Pi Nachkommastellen, die
nicht unter den ersten 200 Mio. Stellen sein sollten (siehe Pi Nachkommastellen §4). 2011 wurden die Fehler beseitigt.
C) pi.nersc.gov
findet das Wort „mir“ erst sehr weit hinten. Dabei kann man beim Zeichensatz 6 schon
ab Index 634 finden: vhmiredgykc siehe Textkonverter Beispiel 4.
vergl. auch Suche Wort in Pi
D) Wolframalpha
findet nicht immer die richtigen Lösungen: siehe Iterationsrechner
Beispiel 50
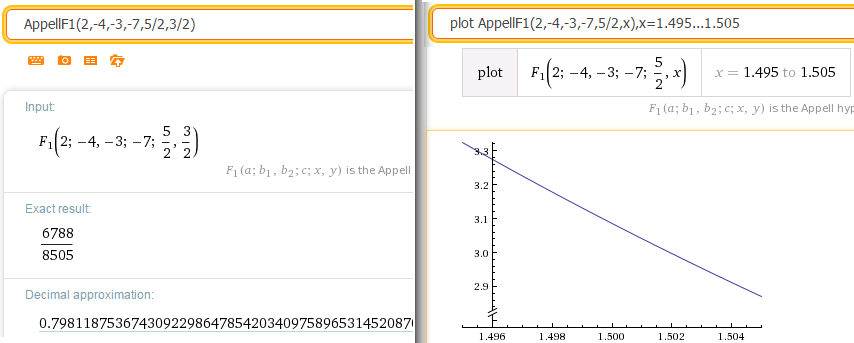
E) AppellF1(2,-4,-3,-7,2.5,1.5): Wolfram
sagt 0.798… und meinen
Berechnungen : laut AppellF1[a, b1, b2, b1 + b2, x, y] = hyg2F1[a, b1, b1 +
b2, (x - y)/(1 - y)]/ (1 - y)^a=AppellF1(-9,-4,0,-7,2/3,3/2)*(1-3/2)^(3-7-2)*(1-2.5)^(4) = 108/35
= 3.0857…
F) Dieser Text wurde zig mal falsch
abgeschrieben: http://www.zeitzuleben.de/13184-ich-bin-faul-und-das-ist-auch-gut-so/
http://www.a2-freun.de/forum/showthread.php?t=43145
http://www.oldendorf-luhe.de/leichtlustig/index.html
Die Suche nach "Setzen
wir nun die unter Kollegen und Vorgesetzen gern genutzten einfachen Worte in
Zahlen um und addieren diese" ergibt über 3000 Ergebnisse!!
Mit dem Iterationsrechner (Parameter
schon im LINK nur Text muss in Feld TXTIN eingegeben werden) kann man
nachrechnen:
N ist 14 und nicht
21
ARSCHKRIECHEN
nicht 129 sondern 122
SCHLEIMEN = 19, 3, 8, 12, 5, 9, 13, 5, 14 nicht 102 sondern 88
WISSEN =23, 9, 19, 19, 5, 14 nicht
79 sondern 89
§3: Unbestimmter_Ausdruck (0 und Unendlich)
§4: Polstellen, Definitionslücke siehe auch Gamma(-n) für ganze n
§5: Nicht jede Division durch 0 ist immer undefiniert -> hebbare Definitionslücke und
Hebbarkeitssatz
siehe auch sinc(x) = sin(x)/x = (x-x³/6+x^5/120-...)/x = 1-x²/6+x^4/120-...
§6: Nicht jede Gleichung hat nur 1 Lösung!
-> oft auch komplexe Lösungen LambertW Beispiele
oder Scheinlösungen -> Probe wichtig!
§7: Die Rekursionstiefe von Rechnern oder Browsern ist nicht konstant! Ein Update kann zu anderen Ergebnissen führen!
Iterationsrechner Beispiel 46 zeigt bei ein und der selben Aufgabe unterschiedliche Obergrenzen!
InternetExplorer7 RT=504; IE8 RT=1286; FireFox 3 RT=677; FireFox 4 RT=263; IE9 RT>1387; FireFox 5 RT=218
§8: endliche Zahlenfolgen ohne Randbedingungen haben nicht nur eine Lösung (Bildungsgesetz)
http://www.testedich.de/quiz04/dasquiztd.php3?testid=1037574607
Frage 13 ergibt erst ein Punkt, wenn man
100010 ankreuzt:
Hier hat sich doch bestimmt ein Fehler eingeschlichen, denn
die Folge
11, 111, 1100, 10010, 11001, 100001,...
ist viel einfacher, als die Lösung wo man einen „Richtig-Punkt“
bekommt:
11, 111, 1100, 10010, 11001, 100010,...
(beide Algorithmen auch unter Zahlenfolgen.html mit
Lösung angegeben)
Folge 1, 8, 27, 64, 125,... kann nicht nur n³ sein, sondern auch
(x*(x*(x*((x-10)*x+155)+310)+384)+120)/120 oder Fak(i)+i*(i*((70-9*i)*i-15)+122)/24; mit Fak(i) = i! (Fakultät)
§9: Rundungsfehler und Fehlerfortpflanzung
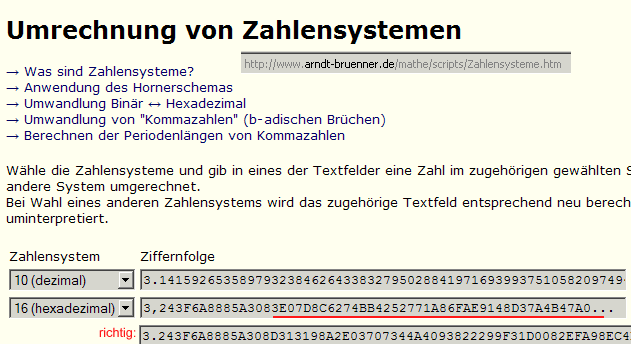
A) Wer hätte gedacht, dass hier nur so wenig Stellen
stimmen:
§10 Brünner’s Approximation von
Dezimalbrüchen durch echte Brüche -> auf Anfrage
§11 AppellF2 Fehler
im Internet -> auf Anfrage
§12 http://mathworld.wolfram.com/TrigonometryAnglesPi9.html Gleichungen (9) und (10) fehlt abs(x)=|x|=sqrt(re(x)²+im(x)²) also (10) richtig:
sin(pi/9)=|((i-sqrt(3))^(1/3)-(i+sqrt(3))^(1/3))|/(2^(4/3))=sqrt(1-((((1+i*sqrt(3))^(1/3)+(1-i*sqrt(3))^(1/3)))/(2^(4/3)))²)
Gleichung (12) ist richtig
§13: Wolfram gibt bei 2^x/45=floor(2^floor(x)/45) für x=2661 aus, aber 2^2661/45 ist 2.441...24337777777... × 10^799 (Periode 7) also keine ganze Zahl.
(zwar nur Rundungsfehler, aber man muss immer kritisch mit dem Ergebnis umgehen...)
§14 Wolfram gibt bei sum 1/(n*log(n)*(log(log(n)))²) ,n=3 ... inf selbst bei Einstellung mehr Nachkommastellen
statt
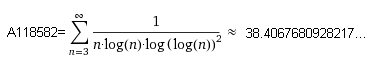
da die extrem langsam konvergierende Summe A118582 10^(3.14*10^86) Summanden für 2 richtige Stellen benötigt!
§15 Unter http://de.wikipedia.org/wiki/Stieltjes-Konstanten steht 1/3 außerhalb der Klammer:
richtig ist innerhalb siehe nichttriviale Grenzwerte §28k
§16 www.testedich.de/quiz31/quiz/1344090651/Mathematik-hohes-Niveau:
inverse {{1,1,1},{1,0,1},{0,0,1}}=[0,1,-1 ; 1,-1,0 ; 0,0,1] und nicht [0,1,-1 ; 1,-1,1 ; 0,0,1]
wie man mit www.arndt-bruenner.de/mathe/scripts/inversematrix.htm
http://werkzeuge.wieschoo.com/invertmat.php
http://de.numberempire.com/matrixcalculator.php und Wolframalpha überprüfen kann
§17 Typisch Mensch: Als Marilyn vos Savant das Ziegenproblem richtig erleuterte (http://de.wikipedia.org/wiki/Marilyn_vos_Savant), "...erhielt sie Tausende von Briefen, deren Absender fast alle darauf bestanden, dass sie Unrecht habe... stellten sich 92% der wissenschaftlich nicht vorgebildeten und immerhin 65% der einer Hochschule angehörenden Leserbriefschreiber gegen sie." Statt wissenschaftlich an eine Sache heranzugehen, wird leider immer noch zuerst versucht, den Überbringer des Wissens umzustimmen...
Iterationsrechner Beispiel 112 zeigt, dass man das leicht per Simulation überprüfen kann.
§18: Vorsicht bei "geht nicht", "gibt's nicht" -> man sollte nicht überhastet "NIE sagen":
Immer wieder wird bis heute behauptet, dass es für die Nullstellen von kubischen und quartischen Gleichungen keine exakte Lösung wie die pq-Formel (oder Mitternachtsformel) für quadratische Gleichung gäbe. Gegenbeweis hier: Quartische_Gleichung (PQRST & PQRSTUVW-Formel) (mit Online-Rechner)
§19: falsche Algorithmen für die Berechnung der Zahl Pi! (also andere Konstante statt A000796)
(vergl. http://www.pimath.de/quadratur/pi_geschichte2.html und http://www.cwscholz.net/projects/fba/#sec_Das Altertum)
a) Bibel (ca. 550 v.Chr.) und Talmud (ca. 500 v.Chr.): "Was im Umfange drei Handbreiten hat, ist eine Hand breit." ...für Pi der Wert 3 angenommen...
b) Der Rabbi Nehemiah gab 150 n.Chr. den Wert für pi mit 3+1/7 an.
c) indische Mathematiker Brahmagupta (geboren 598 n.Chr.): Wurzel aus 10
d) Um 1700 herum war Jacob Marcelis der Meinung, daß es ihm gelungen sei, den Kreis zu quadrieren, und damit den exakten Wert für Pi zu bestimmen:
3+1008449087377541679894282184894/6997183637540819440035239271702 trotz 31stelliger Zähler nicht mal 4 richtige Stellen siehe Zahlenfolgen (Dezimalstellen mathematischer Konstanten)
e) http://mathworld.wolfram.com/AlmostInteger.html "(Borwein and Borwein 1992; Maze and Minder 2005)" fanden eine Konstante, die bei den ersten 18000 Stellen mit Pi übereinstimmt -> also NICHT Pi!
§20: http://de.wikipedia.org/wiki/Russellsche_Antinomie
Gottlob Frege versuchte in seinem Buch "Grundgesetze der Arithmetik von 1893" die Arithmetik auf ein mengentheoretisches Axiomensystem aufzubauen. Die Russellsche Antinomie zeigte, dass dieses Axiomensystem widersprüchlich war. Frege reagierte darauf im Nachwort des zweiten Bands seiner Grundgesetze der Arithmetik von 1903: "Einem wissenschaftlichen Schriftsteller kann kaum etwas Unerwünschteres begegnen, als daß ihm nach Vollendung einer Arbeit eine der Grundlagen seines Baues erschüttert wird. In diese Lage wurde ich durch einen Brief des Herrn Bertrand Russell versetzt, als der Druck dieses Bandes sich seinem Ende näherte."
§21: http://de.wikipedia.org/wiki/Gabriels_Horn
Dieser theoretische Körper mit f(x)=1/x² siehe Volumenintegrale hat in einer Raumdimension die Länge UNENDLICH.
Paradoxon: "Einerseits bräuchte man unendlich viel Farbe, um die Innen- oder Außenfläche des Horns vollständig zu bedecken, andererseits könnte man das Innere des Horns mit einer endlichen Menge Farbe füllen."
Lösung: Es gibt in der Praxis bei der Raumdimension "Länge" weder ein UNENDLICH, noch gibt es Längen, die kleiner als die Planck-Länge (unvorstellbar kleiner als jedes Elementarteilchen) sind! Bereits nach etwa 9 Mio. km hat 1/x etwa die Breite eines Atoms! Dieser Körper muss auch selbst mindestens einige Atomschichten dick sein! (nur ein theoretisch unendlich dünner Körper hat nach Volumenintegraldefinition das Volumen 0)
§22: Manche Prozessoren rechnen falsch: der ASM-Befehl FDIV wurde bei einigen Intel-CPUs falsch implementiert:
4195835/3145727 = 1.3338204491362410024773287701062425315356354826722 und nicht 1,33373907
Iterationsrechner Beispiel 120: große Rundungsfehler einiger FPU: FDIV und FSIN
Grobe FPU Fehler und Genauigkeit von Taschenrechner
§23: http://de.wikipedia.org/wiki/Pentium-F00F-Bug
§24: "%Z" Fehler: einige Interpreter (InTouch) zeigten massive Fehler, wenn im String diese Zeichenfolge vorkam.
§25: der Befehl mem (noch aus DOS Zeiten) in einer BAT Datei etwa 700 mal aufgerufen -> BlueScreen bei Win3.1 bis WinXP ... (bitte nicht nachmachen!)
§26: mein eigener Fehler: bei der Optimierung von hypergeometrischen Funktionen zur schnellen Berechnung von Pi trat an Nachkomma-Stellen um 20000 oder 100000 ein Fehler auf.
Grund: intern rechnete ich mit 64 Bit und es gab Überläufe -> neue CPUs können per DIV-Befehl 2 Register ansprechen, also mit 128Bit Zwischenergebnissen Rechnen -> damit war der Fehler behoben.
§27: Mißachtung des Gültigkeitsbereiches von Algorithmen
§27a) 1+2+3+4+5+6+... = -1/12 findet man zig LINKS (http://www.spiegel.de/wissenschaft/mensch/mathematik-bizarr-summe-aller-natuerlichen-zahlen-ist-negativ-a-944534.html oder https://www.youtube.com/watch?v=w-I6XTVZXww )
Statt 1000 Worte hier die Kurzfassung: für die Riemannsche Zeta Funktion Zeta(x) gibt es unter functions.wolfram 198 Algorithmen.
Wenn man sich nun einen mit eingeschränkten Gültigkeitsbereich herauspickt:
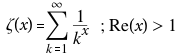und ein dafür ungültiges Argument heraussucht: x=-1(Divergenz: 1/1+1/2^(-1)+1/3^(-1)+... = 1+2+3+... = ∞)
dann ABER einen gültigen Algorithmus verwendet:
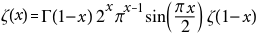
Zeta(-1)=Gamma(2)*2^(-1)*Pi^(-2)*sin(-Pi/2)*Zeta(2)=1*(-1/(2Pi²))*Pi²/6=-1/2*1/6=-1/12
und Teile des ersten Algorithmus mit dem Ergebnis von Zeta(-1) mit einem Gleichheitszeichen verbindet,
kommt diese falsche Gleichheit zustande: 1+2+3+4+... = -1/12
§27b) Fakultät: Fak(x)=x!=1*2*3*...*x für positive ganze x.
Nimmt man nun ein für diesen Algorithmus ungültiges Argument wie x=2.5, kommt nie was gültiges heraus, denn
x!=Gamma(x+1)=Gamma(7/2)=15*sqrt(Pi)/8=3.32335097044784255118406403126464721774540523...
nicht: 1*2.5=2.5
nicht: 1*2*2.5=5 oder andere Mittelwerte...
Egal was man versucht: mit primitiven endlichen Grundrechenarten kommt man nicht auf das richtige irrationale Ergebnis mit unendlich vielen Nachkommastellen!
§27c)
Wenn man eine Reihenentwicklung für tan(x) nimmt
tan(x)=Sum[(((-1)^(k-1)*2^(2k)*(2^(2k)-1)*BernoulliB[2k])/(2k)!)x^(2k-1),k=1...Infinity}]; abs(x)< Pi/2
tan(x)=x+x^3/3+(2 x^5)/15+(17 x^7)/315+(62 x^9)/2835+(1382 x^11)/155925+(21844 x^13)/6081075+...
dann aber den Gültigkeitsbereich missachtet und x größer Pi/2 wählt: x=5Pi/3=5.235987755982988730771...
das in die Reihenformel einsetzt und mit dem Ergebnis von tan(5Pi/3)=-sqrt(3)=-1.732050807568877293527446...
gleichsetzt:
(5Pi)/3+(125Pi³)/81+(1250Pi^5)/729+(265625Pi^7)/137781+(24218750Pi^9)/11160261+...=-sqrt(3)
bekommt man auch so eine falsche Gleichung heraus:
UNENDLICH = -Wurzel(3)
§28 Weg-Zeit-Gesetz-Bremsen-Beschleunigung.htm
§29 Aufgabe aus Begleitheft eines Taschenrechners TI84 und wie die Aufgabe richtig lauten muss!
§30: Viele Rechner berechnen den Divisionsrest (Modulo) von Potenzen nicht oder falsch:
mod(11^(7^8),19) = (11^(7^8)) mod 19 = PowPowMod(11,7,8,19)
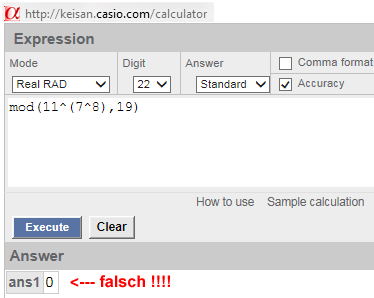
Selbst WolframAlpha rechnet nur bis 4 stellige Argumente (Übergabeparameter).
Deshalb habe ich die PowPowMod()-Funktion hier eingebaut.
§31: Validierung und Verifizierung
Besonders bei der Berechnung von vielen Nachkommastellen wichtig. Es kann einen Überlauf bei Zwischenergebnissen geben...
Es gibt sogar falsche mathematische Algorithmen: eine Konstante stimmte mit über 18000 Nachkommastellen von Pi überein, war aber nicht Pi!
LINKS:
Vermutung (ist noch kein Irrtum)
© Gerd Lamprecht 2012...2016